Journal Description
Current Oncology
Current Oncology
is an international, peer-reviewed, open access journal published online by MDPI (from Volume 28 Issue 1-2021). Established in 1994, the journal represents a multidisciplinary medium for clinical oncologists to report and review progress in the management of this disease. The Canadian Association of Medical Oncologists (CAMO), the Canadian Association of Psychosocial Oncology (CAPO), the Canadian Association of General Practitioners in Oncology (CAGPO), the Cell Therapy Transplant Canada (CTTC), the Canadian Leukemia Study Group (CLSG) and others are affiliated with the journal and their members receive a discount on the article processing charges.
- Open Access— free for readers, with article processing charges (APC) paid by authors or their institutions.
- High Visibility: indexed within Scopus, SCIE (Web of Science), PubMed, MEDLINE, PMC, Embase, and other databases.
- Rapid Publication: manuscripts are peer-reviewed and a first decision is provided to authors approximately 18 days after submission; acceptance to publication is undertaken in 2.8 days (median values for papers published in this journal in the second half of 2023).
- Recognition of Reviewers: APC discount vouchers, optional signed peer review, and reviewer names published annually in the journal.
Impact Factor:
2.6 (2022);
5-Year Impact Factor:
2.9 (2022)
Latest Articles
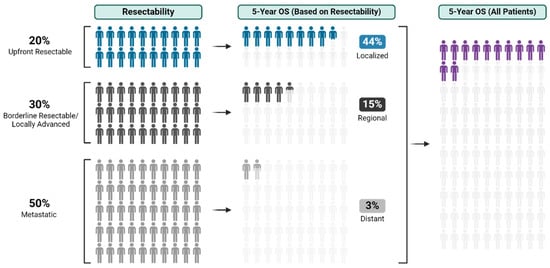
Multimodal Approaches to Patient Selection for Pancreas Cancer Surgery
Curr. Oncol. 2024, 31(4), 2260-2273; https://doi.org/10.3390/curroncol31040167 (registering DOI) - 15 Apr 2024
Abstract
With an overall 5-year survival rate of 12%, pancreas ductal adenocarcinoma (PDAC) is an aggressive cancer that claims more than 50,000 patient lives each year in the United States alone. Even those few patients who undergo curative-intent resection with favorable pathology reports are
[...] Read more.
With an overall 5-year survival rate of 12%, pancreas ductal adenocarcinoma (PDAC) is an aggressive cancer that claims more than 50,000 patient lives each year in the United States alone. Even those few patients who undergo curative-intent resection with favorable pathology reports are likely to experience recurrence within the first two years after surgery and ultimately die from their cancer. We hypothesize that risk factors for these early recurrences can be identified with thorough preoperative staging, thus enabling proper patient selection for surgical resection and avoiding unnecessary harm. Herein, we review evidence supporting multidisciplinary and multimodality staging, comprehensive neoadjuvant treatment strategies, and optimal patient selection for curative-intent surgical resections. We further review data generated from our standardized approach at the Mayo Clinic and extrapolate to inform potential future investigations.
Full article
(This article belongs to the Special Issue New Treatments in Pancreatic Ductal Adenocarcinoma)
►
Show Figures
Open AccessArticle
An Evaluation of Racial and Ethnic Representation in Research Conducted with Young Adults Diagnosed with Cancer: Challenges and Considerations for Building More Equitable and Inclusive Research Practices
by
Sharon H. J. Hou, Fiona S. M. Schulte, Anika Petrella, Joshua Tulk, Amanda Wurz, Catherine M. Sabiston, Jackie Bender, Norma D’Agostino, Karine Chalifour, Geoff Eaton and Sheila N. Garland
Curr. Oncol. 2024, 31(4), 2244-2259; https://doi.org/10.3390/curroncol31040166 (registering DOI) - 15 Apr 2024
Abstract
The psychosocial outcomes of adolescents and young adults (AYAs) diagnosed with cancer are poorer compared to their peers without cancer. However, AYAs with cancer from diverse racial and ethnic groups have been under-represented in research, which contributes to an incomplete understanding of the
[...] Read more.
The psychosocial outcomes of adolescents and young adults (AYAs) diagnosed with cancer are poorer compared to their peers without cancer. However, AYAs with cancer from diverse racial and ethnic groups have been under-represented in research, which contributes to an incomplete understanding of the psychosocial outcomes of all AYAs with cancer. This paper evaluated the racial and ethnic representation in research on AYAs diagnosed with cancer using observational, cross-sectional data from the large Young Adults with Cancer in Their Prime (YACPRIME) study. The purpose was to better understand the psychosocial outcomes for those from diverse racial and ethnic groups. A total of 622 participants with a mean age of 34.15 years completed an online survey, including measures of post-traumatic growth, quality of life, psychological distress, and social support. Of this sample, 2% (n = 13) of the participants self-identified as Indigenous, 3% (n = 21) as Asian, 3% (n = 20) as “other,” 4% (n = 25) as multi-racial, and 87% (n = 543) as White. A one-way ANOVA indicated a statistically significant difference between racial and ethnic groups in relation to spiritual change, a subscale of post-traumatic growth, F(4,548) = 6.02, p < 0.001. Post hoc analyses showed that those under the “other” category endorsed greater levels of spiritual change than those who identified as multi-racial (p < 0.001, 95% CI = [2.49,7.09]) and those who identified as White (p < 0.001, 95% CI = [1.60,5.04]). Similarly, participants that identified as Indigenous endorsed greater levels of spiritual change than those that identified as White (p = 0.03, 95% CI = [1.16,4.08]) and those that identified as multi-racial (p = 0.005, 95% CI = [1.10,6.07]). We provided an extensive discussion on the challenges and limitations of interpreting these findings, given the unequal and small sample sizes across groups. We concluded by outlining key recommendations for researchers to move towards greater equity, inclusivity, and culturally responsiveness in future work.
Full article
(This article belongs to the Section Childhood, Adolescent and Young Adult Oncology)
Open AccessArticle
Survival Outcome Prediction in Glioblastoma: Insights from MRI Radiomics
by
Effrosyni I. Styliara, Loukas G. Astrakas, George Alexiou, Vasileios G. Xydis, Anastasia Zikou, Georgios Kafritsas, Spyridon Voulgaris and Maria I. Argyropoulou
Curr. Oncol. 2024, 31(4), 2233-2243; https://doi.org/10.3390/curroncol31040165 (registering DOI) - 14 Apr 2024
Abstract
►▼
Show Figures
Background: Extracting multiregional radiomic features from multiparametric MRI for predicting pretreatment survival in isocitrate dehydrogenase (IDH) wild-type glioblastoma (GBM) patients is a promising approach. Methods: MRI data from 49 IDH wild-type glioblastoma patients pre-treatment were utilized. Diffusion and perfusion maps were generated, and
[...] Read more.
Background: Extracting multiregional radiomic features from multiparametric MRI for predicting pretreatment survival in isocitrate dehydrogenase (IDH) wild-type glioblastoma (GBM) patients is a promising approach. Methods: MRI data from 49 IDH wild-type glioblastoma patients pre-treatment were utilized. Diffusion and perfusion maps were generated, and tumor subregions segmented. Radiomic features were extracted for each tissue type and map. Feature selection on 1862 radiomic features identified 25 significant features. The Cox proportional-hazards model with LASSO regularization was used to perform survival analysis. Internal and external validation used a 38-patient training cohort and an 11-patient validation cohort. Statistical significance was set at p < 0.05. Results: Age and six radiomic features (shape and first and second order) from T1W, diffusion, and perfusion maps contributed to the final model. Findings suggest that a small necrotic subregion, inhomogeneous vascularization in the solid non-enhancing subregion, and edema-related tissue damage in the enhancing and edema subregions are linked to poor survival. The model’s C-Index was 0.66 (95% C.I. 0.54–0.80). External validation demonstrated good accuracy (AUC > 0.65) at all time points. Conclusions: Radiomics analysis, utilizing segmented perfusion and diffusion maps, provide predictive indicators of survival in IDH wild-type glioblastoma patients, revealing associations with microstructural and vascular heterogeneity in the tumor.
Full article
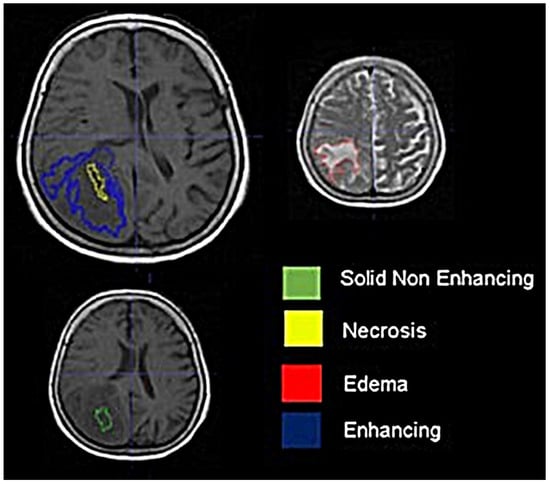
Figure 1
Open AccessArticle
The Level of Agreement between Self-Assessments and Examiner Assessments of Melanocytic Nevus Counts: Findings from an Evaluation of 4548 Double Assessments
by
Olaf Gefeller, Isabelle Kaiser, Emily M. Brockmann, Wolfgang Uter and Annette B. Pfahlberg
Curr. Oncol. 2024, 31(4), 2221-2232; https://doi.org/10.3390/curroncol31040164 (registering DOI) - 13 Apr 2024
Abstract
Cutaneous melanoma (CM) is a candidate for screening programs because its prognosis is excellent when diagnosed at an early disease stage. Targeted screening of those at high risk for developing CM, a cost-effective alternative to population-wide screening, requires valid procedures to identify the
[...] Read more.
Cutaneous melanoma (CM) is a candidate for screening programs because its prognosis is excellent when diagnosed at an early disease stage. Targeted screening of those at high risk for developing CM, a cost-effective alternative to population-wide screening, requires valid procedures to identify the high-risk group. Self-assessment of the number of nevi has been suggested as a component of such procedures, but its validity has not yet been established. We analyzed the level of agreement between self-assessments and examiner assessments of the number of melanocytic nevi in the area between the wrist and the shoulder of both arms based on 4548 study subjects in whom mutually blinded double counting of nevi was performed. Nevus counting followed the IARC protocol. Study subjects received written instructions, photographs, a mirror, and a “nevometer” to support self-assessment of nevi larger than 2 mm. Nevus counts were categorized based on the quintiles of the distribution into five levels, defining a nevus score. Cohen’s weighted kappa coefficient (κ) was estimated to measure the level of agreement. In the total sample, the agreement between self-assessments and examiner assessments was moderate (weighted κ = 0.596). Self-assessed nevus counts were higher than those determined by trained examiners (mean difference: 3.33 nevi). The level of agreement was independent of sociodemographic and cutaneous factors; however, participants’ eye color had a significant impact on the level of agreement. Our findings show that even with comprehensive guidance, only a moderate level of agreement between self-assessed and examiner-assessed nevus counts can be achieved. Self-assessed nevus information does not appear to be reliable enough to be used in individual risk assessment to target screening activities.
Full article
(This article belongs to the Special Issue Epidemiology and Risk Factors of Skin Cancer)
►▼
Show Figures
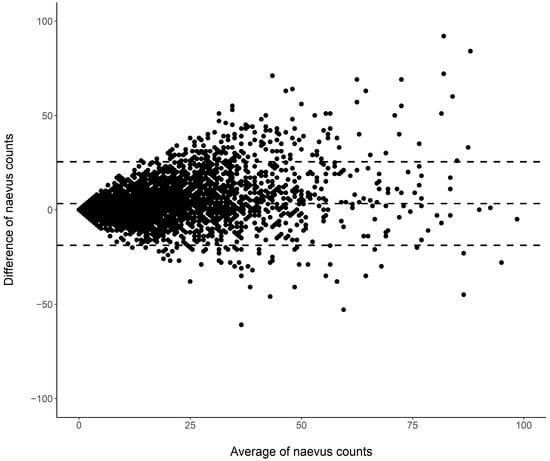
Figure 1
Open AccessSystematic Review
Active Surveillance in Non-Muscle Invasive Bladder Cancer, the Potential Role of Biomarkers: A Systematic Review
by
Diego Parrao, Nemecio Lizana, Catalina Saavedra, Matías Larrañaga, Carolina B. Lindsay, Ignacio F. San Francisco and Juan Cristóbal Bravo
Curr. Oncol. 2024, 31(4), 2201-2220; https://doi.org/10.3390/curroncol31040163 - 12 Apr 2024
Abstract
Bladder cancer (BC) is the tenth most common cause of cancer worldwide and is the thirteenth leading cause of cancer mortality. The non-muscle invasive (NMI) variant represents 75% of cases and has a mortality rate of less than 1%; however, it has a
[...] Read more.
Bladder cancer (BC) is the tenth most common cause of cancer worldwide and is the thirteenth leading cause of cancer mortality. The non-muscle invasive (NMI) variant represents 75% of cases and has a mortality rate of less than 1%; however, it has a high recurrence rate. The gold standard of management is transurethral resection in the case of new lesions. However, this is associated with significant morbidity and costs, so the reduction of these procedures would contribute to reducing complications, morbidity, and the burden to the health system associated with therapy. In this clinical scenario, strategies such as active surveillance have emerged that propose to manage low-risk BC with follow-up; however, due to the low evidence available, this is a strategy that is underutilized by clinicians. On the other hand, in the era of biomarkers, it is increasingly known how to use them as a tool in BC. Therefore, the aim of this review is to provide to clinical practitioners the evidence available to date on AS and the potential role of biomarkers in this therapeutic strategy in patients with low-grade/risk NMIBC. This is the first review linking use of biomarkers and active surveillance, including 29 articles.
Full article
(This article belongs to the Special Issue Surveillance and Active Monitoring Strategies for Cancer: Sometimes Less Is More)
►▼
Show Figures
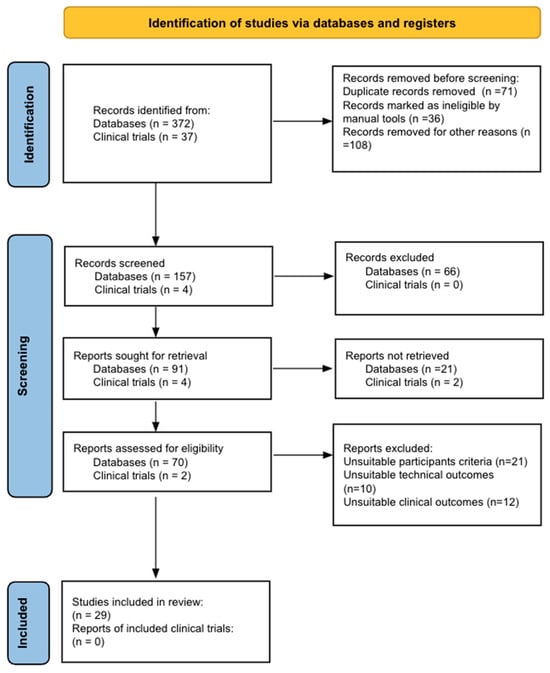
Figure 1
Open AccessReview
Prehabilitation in Adults Undergoing Cancer Surgery: A Comprehensive Review on Rationale, Methodology, and Measures of Effectiveness
by
Carlos E. Guerra-Londono, Juan P. Cata, Katherine Nowak and Vijaya Gottumukkala
Curr. Oncol. 2024, 31(4), 2185-2200; https://doi.org/10.3390/curroncol31040162 - 09 Apr 2024
Abstract
Cancer surgery places a significant burden on a patients’ functional status and quality of life. In addition, cancer surgery is fraught with postoperative complications, themselves influenced by a patient’s functional status. Prehabilitation is a unimodal or multimodal strategy that aims to increase a
[...] Read more.
Cancer surgery places a significant burden on a patients’ functional status and quality of life. In addition, cancer surgery is fraught with postoperative complications, themselves influenced by a patient’s functional status. Prehabilitation is a unimodal or multimodal strategy that aims to increase a patient’s functional capacity to reduce postoperative complications and improve postoperative recovery and quality of life. In most cases, it involves exercise, nutrition, and anxiety-reducing interventions. The impact of prehabilitation has been explored in several types of cancer surgery, most commonly colorectal and thoracic. Overall, the existing evidence suggests prehabilitation improves physiological outcomes (e.g., lean body mass, maximal oxygen consumption) as well as clinical outcomes (e.g., postoperative complications, quality of life). Notably, the benefit of prehabilitation is additional to that of enhanced recovery after surgery (ERAS) programs. While safe, prehabilitation programs require multidisciplinary coordination preoperatively. Despite the existence of numerous systematic reviews and meta-analyses, the certainty of evidence demonstrating the efficacy and safety of prehabilitation is low to moderate, principally due to significant methodological heterogeneity and small sample sizes. There is a need for more large-scale multicenter randomized controlled trials to draw strong clinical recommendations.
Full article
(This article belongs to the Section Surgical Oncology)
►▼
Show Figures
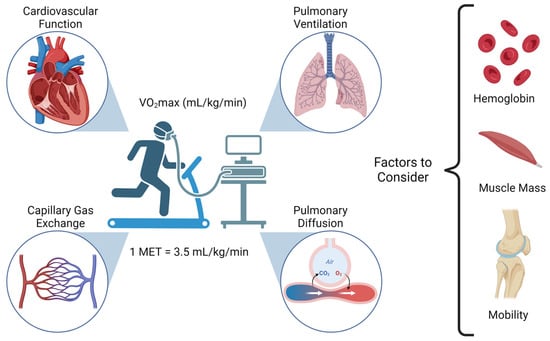
Figure 1
Open AccessArticle
Real-World Treatment Patterns and Clinical Outcomes among Patients Receiving CDK4/6 Inhibitors for Metastatic Breast Cancer in a Canadian Setting Using AI-Extracted Data
by
Ruth Moulson, Guillaume Feugère, Tracy S. Moreira-Lucas, Florence Dequen, Jessica Weiss, Janet Smith and Christine Brezden-Masley
Curr. Oncol. 2024, 31(4), 2172-2184; https://doi.org/10.3390/curroncol31040161 - 09 Apr 2024
Abstract
Cyclin-dependent kinase 4/6 inhibitors (CDK4/6i) are widely used in patients with hormone receptor-positive (HR+)/human epidermal growth factor receptor 2 negative (HER2−) advanced/metastatic breast cancer (ABC/MBC) in first line (1L), but little is known about their real-world use and clinical outcomes long-term, in Canada.
[...] Read more.
Cyclin-dependent kinase 4/6 inhibitors (CDK4/6i) are widely used in patients with hormone receptor-positive (HR+)/human epidermal growth factor receptor 2 negative (HER2−) advanced/metastatic breast cancer (ABC/MBC) in first line (1L), but little is known about their real-world use and clinical outcomes long-term, in Canada. This study used Pentavere’s previously validated artificial intelligence (AI) to extract real-world data on the treatment patterns and outcomes of patients receiving CDK4/6i+endocrine therapy (ET) for HR+/HER2− ABC/MBC at Sinai Health in Toronto, Canada. Between 1 January 2016 and 1 July 2021, 48 patients were diagnosed with HR+/HER2− ABC/MBC and received CDK4/6i + ET. A total of 38 out of 48 patients received CDK4/6i + ET in 1L, of which 34 of the 38 (89.5%) received palbociclib + ET. In 2L, 12 of the 21 (57.1%) patients received CDK4/6i + ET, of which 58.3% received abemaciclib. In 3L, most patients received chemotherapy (10/12, 83.3%). For the patients receiving CDK4/6i in 1L, the median (95% CI) time to the next treatment was 42.3 (41.2, NA) months. The median (95% CI) time to chemotherapy was 46.5 (41.4, NA) months. The two-year overall survival (95% CI) was 97.4% (92.4, 100.0), and the median (range) follow-up was 28.7 (3.4–67.6) months. Despite the limitations inherent in real-world studies and a limited number of patients, these AI-extracted data complement previous studies, demonstrating the effectiveness of CDK4/6i + ET in the Canadian real-world 1L, with most patients receiving palbociclib as CDK4/6i in 1L.
Full article
(This article belongs to the Topic Artificial Intelligence in Cancer, Biology and Oncology)
►▼
Show Figures
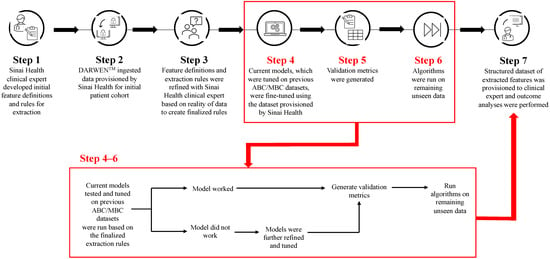
Figure 1
Open AccessReview
The Evaluation and Management of Lung Metastases in Patients with Giant Cell Tumors of Bone in the Denosumab Era
by
Giulia Trovarelli, Arianna Rizzo, Mariachiara Cerchiaro, Elisa Pala, Andrea Angelini and Pietro Ruggieri
Curr. Oncol. 2024, 31(4), 2158-2171; https://doi.org/10.3390/curroncol31040160 - 09 Apr 2024
Abstract
Giant cell tumor of bone (GCTB) is characterized by uncertain biological behavior due to its local aggressiveness and metastasizing potential. In this study, we conducted a meta-analysis of the contemporary literature to evaluate all management strategies for GCTB metastases. A combination of the
[...] Read more.
Giant cell tumor of bone (GCTB) is characterized by uncertain biological behavior due to its local aggressiveness and metastasizing potential. In this study, we conducted a meta-analysis of the contemporary literature to evaluate all management strategies for GCTB metastases. A combination of the terms “lung metastases”, “giant cell tumor”, “bone”, “treatment”, and “oncologic outcomes” returned 133 patients meeting our inclusion criteria: 64 males and 69 females, with a median age of 28 years (7–63), at the onset of primary GCTB. Lung metastases typically occur at a mean interval of 26 months (range: 0–143 months) after treatment of the primary site, commonly presenting as multiple and bilateral lesions. Various treatment approaches, including surgery, chemotherapy, radiotherapy, and drug administration, were employed, while 35 patients underwent routine monitoring only. Upon a mean follow-up of about 7 years (range: 1–32 years), 90% of patients were found to be alive, while 10% had died. Death occurred in 25% of patients who had chemotherapy, whereas 96% of those not treated or treated with Denosumab alone were alive at a mean follow-up of 6 years (range: 1–19 years). Given the typically favorable prognosis of lung metastases in patients with GCTB, additional interventions beyond a histological diagnosis confirmation may not be needed. Denosumab, by reducing the progression of the disease, can play a pivotal role in averting or delaying lung failure.
Full article
(This article belongs to the Special Issue Recent Advances in Diagnosis, Treatment and Prognosis of Giant Cell Tumor of the Bone)
►▼
Show Figures

Figure 1
Open AccessArticle
Evolution of Diagnoses, Survival, and Costs of Oncological Medical Treatment for Non-Small-Cell Lung Cancer over 20 Years in Osona, Catalonia
by
Marta Parera Roig, David Compte Colomé, Gemma Basagaña Colomer, Emilia Gabriela Sardo, Mauricio Alejandro Tournour, Silvia Griñó Fernández, Arturo Ivan Ominetti, Emma Puigoriol Juvanteny, José Luis Molinero Polo, Daniel Badia Jobal and Nadia Espejo-Herrera
Curr. Oncol. 2024, 31(4), 2145-2157; https://doi.org/10.3390/curroncol31040159 - 09 Apr 2024
Abstract
Non-small-cell lung cancer (NSCLC) has experienced several diagnostic and therapeutic changes over the past two decades. However, there are few studies conducted with real-world data regarding the evolution of the cost of these new drugs and the corresponding changes in the survival of
[...] Read more.
Non-small-cell lung cancer (NSCLC) has experienced several diagnostic and therapeutic changes over the past two decades. However, there are few studies conducted with real-world data regarding the evolution of the cost of these new drugs and the corresponding changes in the survival of these patients. We collected data on patients diagnosed with NSCLC from the tumor registry of the University Hospital of Vic from 2002 to 2021. We analyzed the epidemiological and pathological characteristics of these patients, the diverse oncological treatments administered, and the survival outcomes extending at least 18 months post-diagnosis. We also collected data on pharmacological costs, aligning them with the treatments received by each patient to determine the cost associated with individualized treatments. Our study included 905 patients diagnosed with NSCLC. We observed a dynamic shift in histopathological subtypes from squamous carcinoma in the initial years to adenocarcinoma. Regarding the treatment approach, the use of chemotherapy declined over time, replaced by immunotherapy, while molecular therapy showed relative stability. An increase in survival at 18 months after diagnosis was observed in patients with advanced stages over the most recent years of this study, along with the advent of immunotherapy. Mean treatment costs per patient ranged from EUR 1413.16 to EUR 22,029.87 and reached a peak of EUR 48,283.80 in 2017 after the advent of immunotherapy. This retrospective study, based on real-world data, documents the evolution of pathological characteristics, survival rates, and medical treatment costs for NSCLC over the last two decades. After the introduction of immunotherapy, patients in advanced stages showed an improvement in survival at 18 months, coupled with an increase in treatment costs.
Full article
(This article belongs to the Section Thoracic Oncology)
►▼
Show Figures
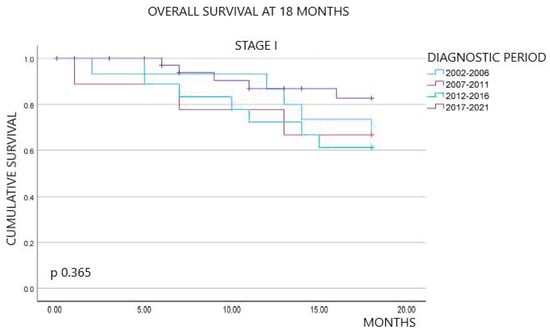
Figure 1
Open AccessArticle
Symptom Burden and Time from Symptom Onset to Cancer Diagnosis in Patients with Early-Onset Colorectal Cancer: A Multicenter Retrospective Analysis
by
Victoria A. Baronas, Arif A. Arif, Eric Bhang, Gale K. Ladua, Carl J. Brown, Fergal Donnellan, Sharlene Gill, Heather C. Stuart and Jonathan M. Loree
Curr. Oncol. 2024, 31(4), 2133-2144; https://doi.org/10.3390/curroncol31040158 - 08 Apr 2024
Abstract
►▼
Show Figures
Background: The incidence of colorectal cancer (CRC) is decreasing in individuals >50 years due to organised screening but has increased for younger individuals. We characterized symptoms and their timing before diagnosis in young individuals. Methods: We identified all patients diagnosed with
[...] Read more.
Background: The incidence of colorectal cancer (CRC) is decreasing in individuals >50 years due to organised screening but has increased for younger individuals. We characterized symptoms and their timing before diagnosis in young individuals. Methods: We identified all patients diagnosed with CRC between 1990–2017 in British Columbia, Canada. Individuals <50 years (n = 2544, EoCRC) and a matched cohort >50 (n = 2570, LoCRC) underwent chart review to identify CRC related symptoms at diagnosis and determine time from symptom onset to diagnosis. Results: Across all stages of CRC, EoCRC presented with significantly more symptoms than LoCRC (Stage 1 mean ± SD: 1.3 ± 0.9 vs. 0.7 ± 0.9, p = 0.0008; Stage 4: 3.3 ± 1.5 vs. 2.3 ± 1.7, p < 0.0001). Greater symptom burden at diagnosis was associated with worse survival in both EoCRC (p < 0.0001) and LoCRC (p < 0.0001). When controlling for cancer stage, both age (HR 0.87, 95% CI 0.8–1.0, p = 0.008) and increasing symptom number were independently associated with worse survival in multivariate models. Conclusions: Patients with EoCRC present with a greater number of symptoms of longer duration than LoCRC; however, time from patient reported symptom onset was not associated with worse outcomes.
Full article
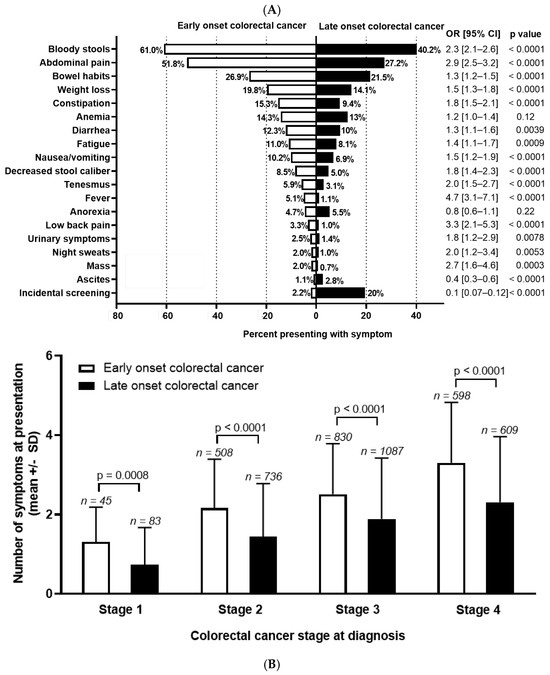
Figure 1
Open AccessReview
Current Concepts in the Treatment of Giant Cell Tumor of Bone: An Update
by
Shinji Tsukamoto, Andreas F. Mavrogenis, Tomoya Masunaga, Kanya Honoki, Hiromasa Fujii, Akira Kido, Yasuhito Tanaka and Costantino Errani
Curr. Oncol. 2024, 31(4), 2112-2132; https://doi.org/10.3390/curroncol31040157 - 08 Apr 2024
Abstract
Curettage is recommended for the treatment of Campanacci stages 1–2 giant cell tumor of bone (GCTB) in the extremities, pelvis, sacrum, and spine, without preoperative denosumab treatment. In the distal femur, bone chips and plate fixation are utilized to reduce damage to the
[...] Read more.
Curettage is recommended for the treatment of Campanacci stages 1–2 giant cell tumor of bone (GCTB) in the extremities, pelvis, sacrum, and spine, without preoperative denosumab treatment. In the distal femur, bone chips and plate fixation are utilized to reduce damage to the subchondral bone and prevent pathological fracture, respectively. For local recurrence, re-curettage may be utilized when feasible. En bloc resection is an option for very aggressive Campanacci stage 3 GCTB in the extremities, pelvis, sacrum, and spine, combined with 1–3 doses of preoperative denosumab treatment. Denosumab monotherapy once every 3 months is currently the standard strategy for inoperable patients and those with metastatic GCTB. However, in case of tumor growth, a possible malignant transformation should be considered. Zoledronic acid appears to be as effective as denosumab; nevertheless, it is a more cost-effective option. Therefore, zoledronic acid may be an alternative treatment option, particularly in developing countries. Surgery is the mainstay treatment for malignant GCTB.
Full article
(This article belongs to the Section Bone and Soft Tissue Oncology)
►▼
Show Figures
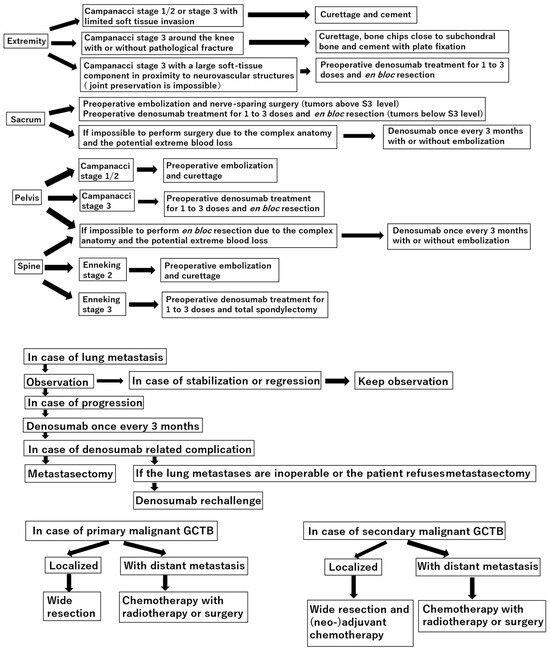
Figure 1
Open AccessEditorial
Innovation and Discovery: A 30-Year Journey in Advancing Cancer Care
by
Shahid Ahmed
Curr. Oncol. 2024, 31(4), 2109-2111; https://doi.org/10.3390/curroncol31040156 - 08 Apr 2024
Abstract
Since the inaugural issue of Current Oncology was published 30 years ago, we have witnessed significant advancements in cancer research and care [...]
Full article
(This article belongs to the Special Issue The 30th Anniversary of Current Oncology: Perspectives in Clinical Oncology Practice)
Open AccessReview
Interdisciplinary Collaboration in Head and Neck Cancer Care: Optimizing Oral Health Management for Patients Undergoing Radiation Therapy
by
Tugce Kutuk, Ece Atak, Alessandro Villa, Noah S. Kalman and Adeel Kaiser
Curr. Oncol. 2024, 31(4), 2092-2108; https://doi.org/10.3390/curroncol31040155 - 07 Apr 2024
Abstract
►▼
Show Figures
Radiation therapy (RT) plays a crucial role in the treatment of head and neck cancers (HNCs). This paper emphasizes the importance of effective communication and collaboration between radiation oncologists and dental specialists in the HNC care pathway. It also provides an overview of
[...] Read more.
Radiation therapy (RT) plays a crucial role in the treatment of head and neck cancers (HNCs). This paper emphasizes the importance of effective communication and collaboration between radiation oncologists and dental specialists in the HNC care pathway. It also provides an overview of the role of RT in HNC treatment and illustrates the interdisciplinary collaboration between these teams to optimize patient care, expedite treatment, and prevent post-treatment oral complications. The methods utilized include a thorough analysis of existing research articles, case reports, and clinical guidelines, with terms such as ‘dental management’, ‘oral oncology’, ‘head and neck cancer’, and ‘radiotherapy’ included for this review. The findings underscore the significance of the early involvement of dental specialists in the treatment planning phase to assess and prepare patients for RT, including strategies such as prophylactic tooth extraction to mitigate potential oral complications. Furthermore, post-treatment oral health follow-up and management by dental specialists are crucial in minimizing the incidence and severity of RT-induced oral sequelae. In conclusion, these proactive measures help minimize dental and oral complications before, during, and after treatment.
Full article

Figure 1
Open AccessReview
Liver-Directed Locoregional Therapies for Neuroendocrine Liver Metastases: Recent Advances and Management
by
Cody R. Criss and Mina S. Makary
Curr. Oncol. 2024, 31(4), 2076-2091; https://doi.org/10.3390/curroncol31040154 - 05 Apr 2024
Abstract
►▼
Show Figures
Neuroendocrine tumors (NETs) are a heterogeneous class of cancers, predominately occurring in the gastroenteropancreatic system, which pose a growing health concern with a significant rise in incidence over the past four decades. Emerging from neuroendocrine cells, these tumors often elicit paraneoplastic syndromes such
[...] Read more.
Neuroendocrine tumors (NETs) are a heterogeneous class of cancers, predominately occurring in the gastroenteropancreatic system, which pose a growing health concern with a significant rise in incidence over the past four decades. Emerging from neuroendocrine cells, these tumors often elicit paraneoplastic syndromes such as carcinoid syndrome, which can manifest as a constellation of symptoms significantly impacting patients’ quality of life. The prognosis of NETs is influenced by their tendency for metastasis, especially in cases involving the liver, where the estimated 5-year survival is between 20 and 40%. Although surgical resection remains the preferred curative option, challenges emerge in cases of neuroendocrine tumors with liver metastasis (NELM) with multifocal lobar involvement, and many patients may not meet the criteria for surgery. Thus, minimally invasive and non-surgical treatments, such as locoregional therapies, have surfaced. Overall, these approaches aim to prioritize symptom relief and aid in overall tumor control. This review examines locoregional therapies, encompassing catheter-driven procedures, ablative techniques, and radioembolization therapies. These interventions play a pivotal role in enhancing progression-free survival and managing hormonal symptoms, contributing to the dynamic landscape of evolving NELM treatment. This review meticulously explores each modality, presenting the current state of the literature on their utilization and efficacy in addressing NELM.
Full article
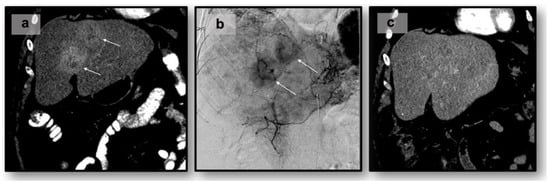
Figure 1
Open AccessCase Report
True Donor Cell Leukemia after Allogeneic Hematopoietic Stem Cell Transplantation: Diagnostic and Therapeutic Considerations—Brief Report
by
Michèle Hoffmann, Yara Banz, Jörg Halter, Jacqueline Schoumans, Joëlle Tchinda, Ulrike Bacher and Thomas Pabst
Curr. Oncol. 2024, 31(4), 2067-2075; https://doi.org/10.3390/curroncol31040153 - 05 Apr 2024
Abstract
Donor cell leukemia (DCL) is a rare complication after allogeneic hematopoietic stem cell transplantation (HSCT) accounting for 0.1% of relapses and presenting as secondary leukemia of donor origin. Distinct in phenotype and cytogenetics from the original leukemia, DCL’s clinical challenge lies in its
[...] Read more.
Donor cell leukemia (DCL) is a rare complication after allogeneic hematopoietic stem cell transplantation (HSCT) accounting for 0.1% of relapses and presenting as secondary leukemia of donor origin. Distinct in phenotype and cytogenetics from the original leukemia, DCL’s clinical challenge lies in its late onset. Its origin is affected by donor cell anomalies, transplant environment, and additional mutations. A 43-year-old woman, treated for early stage triple-negative breast cancer, developed mixed-phenotype acute leukemia (MPAL), 12 years later. Following induction chemotherapy, myeloablative conditioning, and allo-HSCT from her fully HLA-matched brother, she exhibited multiple cutaneous relapses of the original leukemia, subsequently evolving into DCL of the bone marrow. Cytogenetic analysis revealed a complex male karyotype in 20 out of 21 metaphases, however, still showing the MPAL phenotype. DCL diagnosis was confirmed by 90.5% XY in FISH analysis and the male karyotype. Declining further intensive chemotherapy including a second allo-HSCT, she was subsequently treated with repeated radiotherapy, palliative systemic therapies, and finally venetoclax and navitoclax but died seven months post-DCL diagnosis. This case underlines DCL’s complexity, characterized by unique genetics, further complicating diagnosis. It highlights the need for advanced diagnostic techniques for DCL identification and underscores the urgency for early detection and better prevention and treatment strategies.
Full article
(This article belongs to the Section Hematology)
►▼
Show Figures
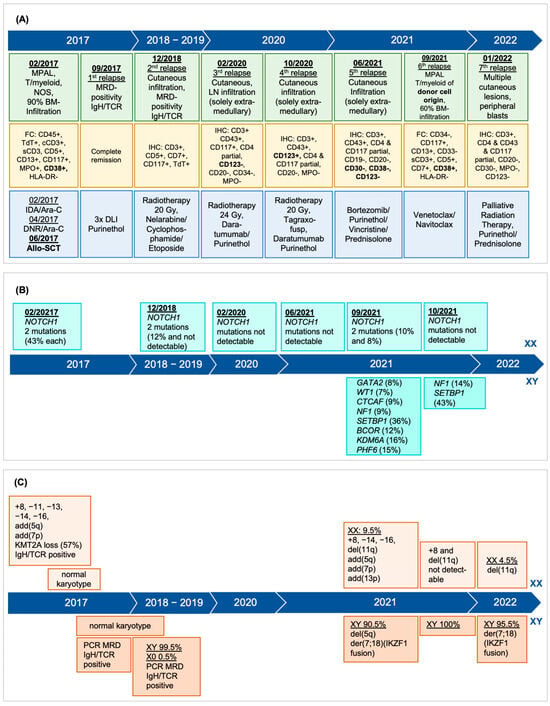
Figure 1
Open AccessSystematic Review
The Efficacy of Fat Grafting on Treating Post-Mastectomy Pain with and without Breast Reconstruction: A Systematic Review and Meta-Analysis
by
Jeffrey Chen, Abdulrahman A. Alghamdi, Chi Yi Wong, Muna F. Alnaim, Gabriel Kuper and Jing Zhang
Curr. Oncol. 2024, 31(4), 2057-2066; https://doi.org/10.3390/curroncol31040152 - 04 Apr 2024
Abstract
Post-mastectomy pain syndrome (PMPS), characterized by persistent pain lasting at least three months following mastectomy, affects 20–50% of breast surgery patients, lacking effective treatment options. A review was conducted utilizing EMBASE, MEDLINE, and all evidence-based medicine reviews to evaluate the effect of fat
[...] Read more.
Post-mastectomy pain syndrome (PMPS), characterized by persistent pain lasting at least three months following mastectomy, affects 20–50% of breast surgery patients, lacking effective treatment options. A review was conducted utilizing EMBASE, MEDLINE, and all evidence-based medicine reviews to evaluate the effect of fat grafting as a treatment option for PMPS from database inception to 29 April 2023 (PROSPERO ID: CRD42023422627). Nine studies and 812 patients in total were included in the review. The overall mean change in visual analog scale (VAS) was −3.6 in 285 patients following fat grafting and 0.5 in 147 control group patients. There was a significant reduction in VAS from baseline in the fat grafting group compared to the control group, n = 395, mean difference = −2.17 (95% CI, −2.95 to −1.39). This significant improvement was also noted in patients who underwent mastectomy without reconstruction. Common complications related to fat grafting include capsular contracture, seroma, hematoma, and infection. Surgeons should consider fat grafting as a treatment option for PMPS. However, future research is needed to substantiate this evidence and to identify timing, volume of fat grafting, and which patient cohort will benefit the most.
Full article
(This article belongs to the Section Surgical Oncology)
►▼
Show Figures
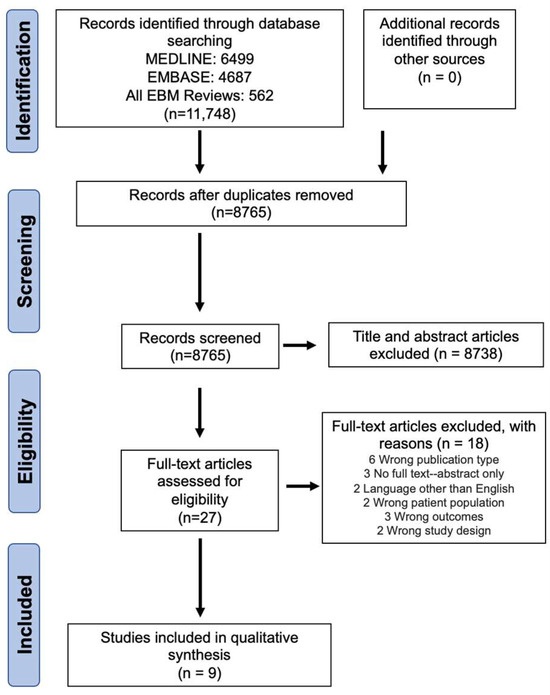
Figure 1
Open AccessCase Report
Preoperative Direct Puncture Embolization of Castleman Disease of the Parotid Gland: A Case Report
by
Alessandro Pedicelli, Pietro Trombatore, Andrea Bartolo, Arianna Camilli, Esther Diana Rossi, Luca Scarcia and Andrea M. Alexandre
Curr. Oncol. 2024, 31(4), 2047-2056; https://doi.org/10.3390/curroncol31040151 - 04 Apr 2024
Abstract
Background: Castleman disease (CD) is an uncommon benign lymphoproliferative disease characterized by hypervascular lymphoid hyperplasia. We present a unique case of unicentric CD of the parotid gland treated by preoperative direct puncture embolization. Case presentation: A 27-year-old female patient was admitted for a
[...] Read more.
Background: Castleman disease (CD) is an uncommon benign lymphoproliferative disease characterized by hypervascular lymphoid hyperplasia. We present a unique case of unicentric CD of the parotid gland treated by preoperative direct puncture embolization. Case presentation: A 27-year-old female patient was admitted for a right neck mass. Ultrasound examination and MRI scan documented a hypervascular mass within the right parotid gland. Preoperative embolization was performed by direct puncture technique: a needle was inserted into the core of the mass under both ultrasound and fluoroscopic guidance and SQUID 12 was injected into the mass under fluoroscopic control, achieving a total devascularization. Conclusion: Preoperative direct puncture embolization was safe and effective and provides excellent hemostatic control during the surgical operation, limiting the amount of intraoperative bleeding.
Full article
(This article belongs to the Section Head and Neck Oncology)
►▼
Show Figures

Figure 1
Open AccessReview
KRAS: Biology, Inhibition, and Mechanisms of Inhibitor Resistance
by
Leonard J. Ash, Ottavia Busia-Bourdain, Daniel Okpattah, Avrosina Kamel, Ariel Liberchuk and Andrew L. Wolfe
Curr. Oncol. 2024, 31(4), 2024-2046; https://doi.org/10.3390/curroncol31040150 - 03 Apr 2024
Abstract
►▼
Show Figures
KRAS is a small GTPase that is among the most commonly mutated oncogenes in cancer. Here, we discuss KRAS biology, therapeutic avenues to target it, and mechanisms of resistance that tumors employ in response to KRAS inhibition. Several strategies are under investigation for
[...] Read more.
KRAS is a small GTPase that is among the most commonly mutated oncogenes in cancer. Here, we discuss KRAS biology, therapeutic avenues to target it, and mechanisms of resistance that tumors employ in response to KRAS inhibition. Several strategies are under investigation for inhibiting oncogenic KRAS, including small molecule compounds targeting specific KRAS mutations, pan-KRAS inhibitors, PROTACs, siRNAs, PNAs, and mutant KRAS-specific immunostimulatory strategies. A central challenge to therapeutic effectiveness is the frequent development of resistance to these treatments. Direct resistance mechanisms can involve KRAS mutations that reduce drug efficacy or copy number alterations that increase the expression of mutant KRAS. Indirect resistance mechanisms arise from mutations that can rescue mutant KRAS-dependent cells either by reactivating the same signaling or via alternative pathways. Further, non-mutational forms of resistance can take the form of epigenetic marks, transcriptional reprogramming, or alterations within the tumor microenvironment. As the possible strategies to inhibit KRAS expand, understanding the nuances of resistance mechanisms is paramount to the development of both enhanced therapeutics and innovative drug combinations.
Full article

Graphical abstract
Open AccessCase Report
The Potential of Integrative Cancer Treatment Using Melatonin and the Challenge of Heterogeneity in Population-Based Studies: A Case Report of Colon Cancer and a Literature Review
by
Eugeniy Smorodin, Valentin Chuzmarov and Toomas Veidebaum
Curr. Oncol. 2024, 31(4), 1994-2023; https://doi.org/10.3390/curroncol31040149 - 03 Apr 2024
Abstract
Melatonin is a multifunctional hormone regulator that maintains homeostasis through circadian rhythms, and desynchronization of these rhythms can lead to gastrointestinal disorders and increase the risk of cancer. Preliminary clinical studies have shown that exogenous melatonin alleviates the harmful effects of anticancer therapy
[...] Read more.
Melatonin is a multifunctional hormone regulator that maintains homeostasis through circadian rhythms, and desynchronization of these rhythms can lead to gastrointestinal disorders and increase the risk of cancer. Preliminary clinical studies have shown that exogenous melatonin alleviates the harmful effects of anticancer therapy and improves quality of life, but the results are still inconclusive due to the heterogeneity of the studies. A personalized approach to testing clinical parameters and response to integrative treatment with nontoxic and bioavailable melatonin in patient-centered N-of-1 studies deserves greater attention. This clinical case of colon cancer analyzes and discusses the tumor pathology, the adverse effects of chemotherapy, and the dynamics of markers of inflammation (NLR, LMR, and PLR ratios), tumors (CEA, CA 19-9, and PSA), and hemostasis (D-dimer and activated partial thromboplastin time). The patient took melatonin during and after chemotherapy, nutrients (zinc, selenium, vitamin D, green tea, and taxifolin), and aspirin after chemotherapy. The patient’s PSA levels decreased during CT combined with melatonin (19 mg/day), and melatonin normalized inflammatory markers and alleviated symptoms of polyneuropathy but did not help with thrombocytopenia. The results are analyzed and discussed in the context of the literature on oncostatic and systemic effects, alleviating therapy-mediated adverse effects, association with survival, and N-of-1 studies.
Full article
(This article belongs to the Section Gastrointestinal Oncology)
►▼
Show Figures

Figure 1
Open AccessReview
Myelodysplastic Neoplasms (MDS): The Current and Future Treatment Landscape
by
Daniel Karel, Claire Valburg, Navitha Woddor, Victor E. Nava and Anita Aggarwal
Curr. Oncol. 2024, 31(4), 1971-1993; https://doi.org/10.3390/curroncol31040148 - 03 Apr 2024
Abstract
Myelodysplastic neoplasms (MDS) are a heterogenous clonal disorder of hemopoietic stem cells characterized by cytomorphologic dysplasia, ineffective hematopoiesis, peripheral cytopenias and risk of progression to acute myeloid leukemia (AML). Our understanding of this disease has continued to evolve over the last century. More
[...] Read more.
Myelodysplastic neoplasms (MDS) are a heterogenous clonal disorder of hemopoietic stem cells characterized by cytomorphologic dysplasia, ineffective hematopoiesis, peripheral cytopenias and risk of progression to acute myeloid leukemia (AML). Our understanding of this disease has continued to evolve over the last century. More recently, prognostication and treatment have been determined by cytogenetic and molecular data. Specific genetic abnormalities, such as deletion of the long arm of chromosome 5 (del(5q)), TP53 inactivation and SF3B1 mutation, are increasingly associated with disease phenotype and outcome, as reflected in the recently updated fifth edition of the World Health Organization Classification of Hematolymphoid Tumors (WHO5) and the International Consensus Classification 2022 (ICC 2022) classification systems. Treatment of lower-risk MDS is primarily symptom directed to ameliorate cytopenias. Higher-risk disease warrants disease-directed therapy at diagnosis; however, the only possible cure is an allogenic bone marrow transplant. Novel treatments aimed at rational molecular and cellular pathway targets have yielded a number of candidate drugs over recent years; however few new approvals have been granted. With ongoing research, we hope to increasingly offer our MDS patients tailored therapeutic approaches, ultimately decreasing morbidity and mortality.
Full article
(This article belongs to the Section Hematology)

Journal Menu
► ▼ Journal Menu-
- Current Oncology Home
- Aims & Scope
- Editorial Board
- Reviewer Board
- Topical Advisory Panel
- Instructions for Authors
- Special Issues
- Topics
- Sections & Collections
- Article Processing Charge
- Indexing & Archiving
- Editor’s Choice Articles
- Most Cited & Viewed
- Journal Statistics
- Journal History
- Journal Awards
- Society Collaborations
- Conferences
- Editorial Office
Journal Browser
► ▼ Journal Browser-
arrow_forward_ios
Forthcoming issue
arrow_forward_ios Current issue - Volumes not published by MDPI
Highly Accessed Articles
Latest Books
E-Mail Alert
News
Topics
Topic in
Biomedicines, BioMedInformatics, Cancers, JCM, Cells, Current Oncology
Cancer Immunity and Immunotherapy: Early Detection, Diagnosis, Systemic Treatments, Novel Biomarkers, and Resistance Mechanisms
Topic Editors: Tao Jiang, Yongchang ZhangDeadline: 20 April 2024
Topic in
Biology, Cancers, Current Oncology, Diseases, JCM, Pathogens
Pathogenetic, Diagnostic and Therapeutic Perspectives in Head and Neck Cancer
Topic Editors: Shun-Fa Yang, Ming-Hsien ChienDeadline: 20 June 2024
Topic in
Cancers, Cells, JCM, Radiation, Pharmaceutics, Applied Sciences, Nanomaterials, Current Oncology
Innovative Radiation Therapies
Topic Editors: Gérard Baldacchino, Eric Deutsch, Marie Dutreix, Sandrine Lacombe, Erika Porcel, Charlotte Robert, Emmanuelle Bourneuf, João Santos Sousa, Aurélien de la LandeDeadline: 30 June 2024
Topic in
Cancers, Diagnostics, JCM, Current Oncology, Gastrointestinal Disorders, Biomedicines
Hepatobiliary and Pancreatic Diseases: Novel Strategies of Diagnosis and Treatments
Topic Editors: Alessandro Coppola, Damiano Caputo, Roberta Angelico, Domenech Asbun, Chiara MazzarelliDeadline: 20 July 2024

Conferences
Special Issues
Special Issue in
Current Oncology
The Clinical Trials and Management of Acute Myeloid Leukemia
Guest Editor: Margaret T. KasnerDeadline: 26 April 2024
Special Issue in
Current Oncology
Liver Transplantation for Cancer: The Future of Transplant Oncology
Guest Editor: Tomoharu YoshizumiDeadline: 30 April 2024
Special Issue in
Current Oncology
An Update on Surgical Treatment for Hepato-Pancreato-Biliary Cancers
Guest Editors: Nikolaos Machairas, Stylianos Kykalos, Dimitrios SchizasDeadline: 15 May 2024
Special Issue in
Current Oncology
Surgery Advances in Gynecologic Tumors
Guest Editor: Allan L. CovensDeadline: 31 May 2024
Topical Collections
Topical Collection in
Current Oncology
Editorial Board Members’ Collection Series: Contemporary Perioperative Concepts in Cancer Surgery
Collection Editors: Vijaya Gottumukkala, Jörg Kleeff
Topical Collection in
Current Oncology
Editorial Board Members’ Collection Series in "Exercise and Cancer Management"
Collection Editors: Linda Denehy, Ravi Mehrotra, Nicole Culos-Reed
Topical Collection in
Current Oncology
New Insights into Prostate Cancer Diagnosis and Treatment
Collection Editor: Sazan Rasul
Topical Collection in
Current Oncology
New Insights into Breast Cancer Diagnosis and Treatment
Collection Editors: Filippo Pesapane, Matteo Suter