Journal Description
Current Oncology
Current Oncology
is an international, peer-reviewed, open access journal published online by MDPI (from Volume 28 Issue 1-2021). Established in 1994, the journal represents a multidisciplinary medium for clinical oncologists to report and review progress in the management of this disease. The Canadian Association of Medical Oncologists (CAMO), the Canadian Association of Psychosocial Oncology (CAPO), the Canadian Association of General Practitioners in Oncology (CAGPO), the Cell Therapy Transplant Canada (CTTC), the Canadian Leukemia Study Group (CLSG) and others are affiliated with the journal and their members receive a discount on the article processing charges.
- Open Access— free for readers, with article processing charges (APC) paid by authors or their institutions.
- High Visibility: indexed within Scopus, SCIE (Web of Science), PubMed, MEDLINE, PMC, Embase, and other databases.
- Rapid Publication: manuscripts are peer-reviewed and a first decision is provided to authors approximately 18 days after submission; acceptance to publication is undertaken in 2.8 days (median values for papers published in this journal in the second half of 2023).
- Recognition of Reviewers: APC discount vouchers, optional signed peer review, and reviewer names published annually in the journal.
Impact Factor:
2.6 (2022);
5-Year Impact Factor:
2.9 (2022)
Latest Articles
Patients with Leptomeningeal Carcinomatosis and Hydrocephalus-Feasibility of Combined Ventriculoperitoneal Shunt and Reservoir Insertion for Intrathecal Chemotherapy
Curr. Oncol. 2024, 31(5), 2410-2419; https://doi.org/10.3390/curroncol31050180 (registering DOI) - 24 Apr 2024
Abstract
Therapeutic management of patients with leptomeningeal carcinomatosis (LC) may require treatment of concomitant hydrocephalus (HC) in addition to intrathecal chemotherapy (ITC). Ventriculoperitoneal shunts (VPS) equipped with a valve for manual deactivation of shunt function and a concomitant reservoir for application of ITC pose
[...] Read more.
Therapeutic management of patients with leptomeningeal carcinomatosis (LC) may require treatment of concomitant hydrocephalus (HC) in addition to intrathecal chemotherapy (ITC). Ventriculoperitoneal shunts (VPS) equipped with a valve for manual deactivation of shunt function and a concomitant reservoir for application of ITC pose an elegant solution to both problems. The present study evaluates indication, feasibility, and safety of such a modified shunt/reservoir design (mS/R). All patients with LC aged ≥ 18 years who had undergone mS/R implantation between 2013 and 2020 at the authors’ institution were further analyzed. ITC was indicated following the recommendation of the neuro-oncological tumor board and performed according to a standardized protocol. Sixteen patients with LC underwent mS/R implantation for subsequent ITC and concomitant treatment of HC. Regarding HC-related clinical symptoms, 69% of patients preoperatively exhibited lethargy, 38% cognitive impairment, and 38% (additional) visual disturbances. Postoperatively, 86% of patients achieved subjective improvement of HC-related symptoms. Overall, postoperative complications occurred in three patients (19%). No patient encountered cancer treatment-related complications. The present study describes a combination procedure consisting of a standard VPS-system and a standard reservoir for patients suffering from LC and HC. No cancer treatment-related complications occurred, indicating straightforward handling and thus safety.
Full article
(This article belongs to the Section Neuro-Oncology)
►
Show Figures
Open AccessFeature PaperArticle
Surgery Advances in Gynecologic Tumors: The Evolution and Outcomes of Robotic Surgery for Gynecologic Cancers in a Tertiary Center
by
David Knigin, Yoav Brezinov, Shannon Salvador, Susie Lau and Walter H. Gotlieb
Curr. Oncol. 2024, 31(5), 2400-2409; https://doi.org/10.3390/curroncol31050179 - 24 Apr 2024
Abstract
The integration of innovation into routine clinical practice is faced with many challenges. In 2007, we received the mandate to evaluate how the introduction of a robotic program in gynecologic oncology affected patient-centered care by studying its impact on clinical outcomes and hospital
[...] Read more.
The integration of innovation into routine clinical practice is faced with many challenges. In 2007, we received the mandate to evaluate how the introduction of a robotic program in gynecologic oncology affected patient-centered care by studying its impact on clinical outcomes and hospital resource utilization. Here we summarize the history and experience of developing a robotic surgery program for gynecologic cancers over 16 years. Analysis of the data indicates that robotic surgery improved perioperative patient clinical parameters, decreased blood loss, complications, and hospital stay, maintained the oncologic outcome, and is cost-effective, resulting in it becoming the dominant surgical approach in gynecologic oncology in a tertiary cancer care institution.
Full article
(This article belongs to the Special Issue Surgery Advances in Gynecologic Tumors)
►▼
Show Figures
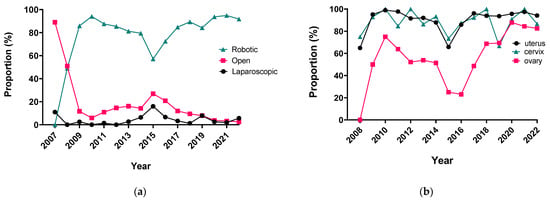
Figure 1
Open AccessCase Report
Mixed Adenosquamous Cell Carcinoma of the Prostate with Paired Sequencing on the Primary and Liver Metastasis
by
Emmanuella Oyogoa, Maya Sonpatki, Brian T. Brinkerhoff, Nicole Andeen, Haley Meyer, Christopher Ryan and Alexandra O. Sokolova
Curr. Oncol. 2024, 31(5), 2393-2399; https://doi.org/10.3390/curroncol31050178 - 24 Apr 2024
Abstract
This report aims to shed light on the intricate challenges encountered during the diagnosis and treatment of an uncommon variant of prostate cancer—mixed adenosquamous cell carcinoma of the prostate. Prostate cancers of this nature pose distinctive diagnostic and therapeutic dilemmas due to their
[...] Read more.
This report aims to shed light on the intricate challenges encountered during the diagnosis and treatment of an uncommon variant of prostate cancer—mixed adenosquamous cell carcinoma of the prostate. Prostate cancers of this nature pose distinctive diagnostic and therapeutic dilemmas due to their rarity and complex histological composition. We present a case of a 63-year-old man with metastatic prostate cancer, featuring adenocarcinoma with squamous cell differentiation, who underwent a multimodal treatment approach. The patient responded to first-line carboplatin, docetaxel, and androgen deprivation therapy, followed by androgen receptor pathway inhibitor (ARPI) maintenance. However, disease progression led to radiation therapy and a subsequent switch to Lutetium (177Lu) vipivotide tetraxetan after chemotherapy challenges. Comprehensive genetic profiling revealed shared mutations in the prostate and liver lesions, emphasizing the role of targeted therapies. Prostate-specific membrane antigen (PSMA)-targeted therapy resulted in a notable PSA decline. This case highlights the evolving treatment landscape for rare prostate cancers, integrating genetic insights for tailored interventions. In conclusion, squamous cell carcinoma (SCC) of the prostate is rare, emphasizing the imperative for enhanced comprehension in diagnosis and management. Our case suggests the potential efficacy of ARPI and PSMA-targeted therapies. Our findings advocate for a more nuanced approach to the management of this rare prostate cancer variant, leveraging genomic insights for personalized treatment strategies. This exploration serves as a foundation for further research and clinical considerations in addressing the challenges posed by mixed adenosquamous cell carcinoma of the prostate.
Full article
(This article belongs to the Topic Prostate Cancer: Symptoms, Diagnosis & Treatment - 2nd Volume)
►▼
Show Figures

Figure 1
Open AccessArticle
12-Month Trajectories of Health-Related Quality of Life Following Hospitalization in German Cancer Centers—A Secondary Data Analysis
by
Martin Eichler, Klaus Hönig, Corinna Bergelt, Hermann Faller, Imad Maatouk, Beate Hornemann, Barbara Stein, Martin Teufel, Ute Goerling, Yesim Erim, Franziska Geiser, Alexander Niecke, Bianca Senf and Joachim Weis
Curr. Oncol. 2024, 31(5), 2376-2392; https://doi.org/10.3390/curroncol31050177 (registering DOI) - 23 Apr 2024
Abstract
►▼
Show Figures
Patient-reported outcomes (PROs) offer a diverse array of potential applications within medical research and clinical practice. In comparative research, they can serve as tools for delineating the trajectories of health-related quality of life (HRQoL) across various cancer types. We undertook a secondary data
[...] Read more.
Patient-reported outcomes (PROs) offer a diverse array of potential applications within medical research and clinical practice. In comparative research, they can serve as tools for delineating the trajectories of health-related quality of life (HRQoL) across various cancer types. We undertook a secondary data analysis of a cohort of 1498 hospitalized cancer patients from 13 German cancer centers. We assessed the Physical and Mental Component Scores (PCS and MCS) of the 12-Item Short-Form Health Survey at baseline (t0), 6 (t1), and 12 months (t2), using multivariable generalized linear regression models. At baseline, the mean PCS and MCS values for all cancer patients were 37.1 and 44.3 points, respectively. We observed a significant improvement in PCS at t2 and in MCS at t1. The most substantial and significant improvements were noted among patients with gynecological cancers. We found a number of significant differences between cancer types at baseline, t1, and t2, with skin cancer patients performing best across all time points and lung cancer patients performing the worst. MCS trajectories showed less pronounced changes and differences between cancer types. Comparative analyses of HRQoL scores across different cancer types may serve as a valuable tool for enhancing health literacy, both among the general public and among cancer patients themselves.
Full article
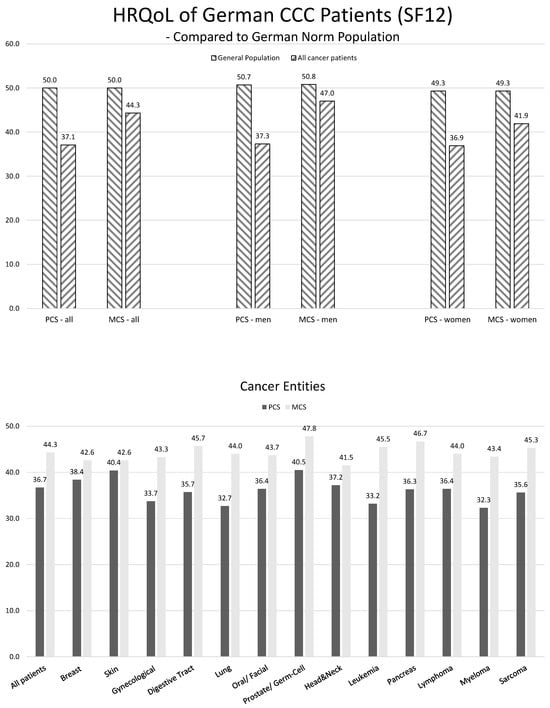
Figure 1
Open AccessReview
The Significance of Thyroid Hormone Receptors in Breast Cancer: A Hypothesis-Generating Narrative Review
by
Trinity Quan, Jessica Cockburn, Sukhbinder Dhesy-Thind, Anita Bane, Hon Leong, Christopher Geleff, Catherine Devion, Noor Ajel and Katarzyna J. Jerzak
Curr. Oncol. 2024, 31(5), 2364-2375; https://doi.org/10.3390/curroncol31050176 - 23 Apr 2024
Abstract
Background: Breast cancer (BC) is frequently diagnosed among Canadian women. While targeted therapies are available for most BC patients; treatment resistance is common and novel therapeutic targets are of interest. Thyroid hormones (TH) bound to thyroid hormone receptors (THR) influence cell proliferation and
[...] Read more.
Background: Breast cancer (BC) is frequently diagnosed among Canadian women. While targeted therapies are available for most BC patients; treatment resistance is common and novel therapeutic targets are of interest. Thyroid hormones (TH) bound to thyroid hormone receptors (THR) influence cell proliferation and differentiation; they are also involved in the growth and development of normal breast tissue. Evidence suggests that THRβ is a tumor suppressor in various solid tumors. Purpose: This narrative review discusses retrospective studies regarding the clinical relevance of THRβ as a potential prognostic biomarker and therapeutic target in BC. Methods: We consulted with an information specialist to develop a search strategy to find all literature related to THRα expression as a potential prognostic and therapeutic biomarker in breast cancer. The primary search was developed for Medline and translated to Embase. The searches were conducted on the Ovid platform on 18 August 2023. Results: Across seven retrospective studies identified, several have shown an association between higher THRβ1 expression with a lower risk of BC recurrence and with longer overall survival. Conclusions: Some evidence suggests that THRβ expression is associated with a lower risk of BC recurrence and death. Validation of THRβ as an independent prognostic biomarker and possible predictive biomarker of response to endocrine therapy and/or chemotherapy is of interest. Given that THRβ is upstream of the AKT/PI3K pathway, its potential as a predictive biomarker of response to AKT inhibitors and/or PI3K inhibitors may also be of value. Finally, the potential re-purposing of THRβ agonists as anti-cancer agents warrants investigation.
Full article
(This article belongs to the Special Issue Advanced Approaches to Breast Cancer Biomarkers)
►▼
Show Figures
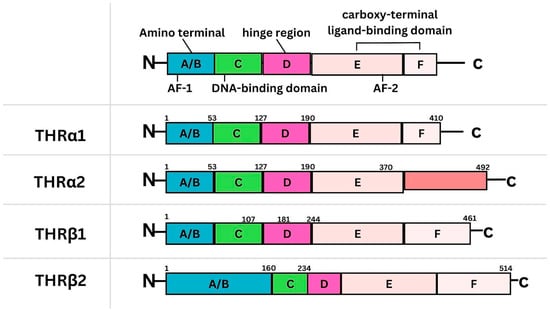
Figure 1
Open AccessReview
A Brief Overview of the Molecular Landscape of Myelodysplastic Neoplasms
by
Rami Abdulbaki and Sheeja T. Pullarkat
Curr. Oncol. 2024, 31(5), 2353-2363; https://doi.org/10.3390/curroncol31050175 - 23 Apr 2024
Abstract
Myelodysplastic neoplasm (MDS) is a heterogeneous group of clonal hematological disorders that originate from the hematopoietic and progenitor cells and present with cytopenias and morphologic dysplasia with a propensity to progress to bone marrow failure or acute myeloid leukemia (AML). Genetic evolution plays
[...] Read more.
Myelodysplastic neoplasm (MDS) is a heterogeneous group of clonal hematological disorders that originate from the hematopoietic and progenitor cells and present with cytopenias and morphologic dysplasia with a propensity to progress to bone marrow failure or acute myeloid leukemia (AML). Genetic evolution plays a critical role in the pathogenesis, progression, and clinical outcomes of MDS. This process involves the acquisition of genetic mutations in stem cells that confer a selective growth advantage, leading to clonal expansion and the eventual development of MDS. With the advent of next-generation sequencing (NGS) assays, an increasing number of molecular aberrations have been discovered in recent years. The knowledge of molecular events in MDS has led to an improved understanding of the disease process, including the evolution of the disease and prognosis, and has paved the way for targeted therapy. The 2022 World Health Organization (WHO) Classification and the International Consensus Classification (ICC) have incorporated the molecular signature into the classification system for MDS. In addition, specific germline mutations are associated with MDS development, especially in pediatrics and young adults. This article reviews the genetic abnormalities of MDS in adults with a brief review of germline predisposition syndromes.
Full article
(This article belongs to the Special Issue The Molecular Pathology of Myelodysplastic Syndromes)
►▼
Show Figures
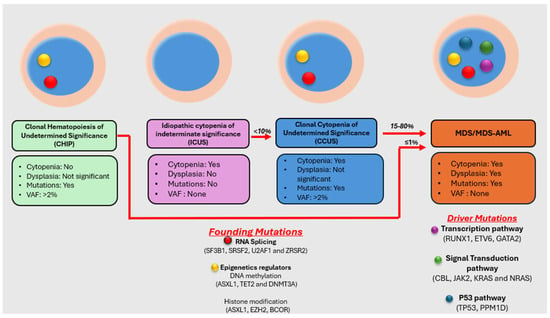
Figure 1
Open AccessReview
Gastro-Intestinal Symptoms in Palliative Care Patients
by
Golda Elisa Tradounsky
Curr. Oncol. 2024, 31(4), 2341-2352; https://doi.org/10.3390/curroncol31040174 - 21 Apr 2024
Abstract
This review of the palliation of various gastro-intestinal (GI) symptoms encountered in cancer patients is by no means exhaustive. Frequent symptoms such as constipation, nausea and vomiting, bowel obstructions, ascites and bleeds will be discussed, focusing on their assessment and most importantly, how
[...] Read more.
This review of the palliation of various gastro-intestinal (GI) symptoms encountered in cancer patients is by no means exhaustive. Frequent symptoms such as constipation, nausea and vomiting, bowel obstructions, ascites and bleeds will be discussed, focusing on their assessment and most importantly, how to control the associated symptoms. All of these symptoms and GI complications can significantly impact patients’ quality of life (QOL) and should be treated as quickly and aggressively as possible.
Full article
(This article belongs to the Special Issue 2023–2024 Article Series of the Canadian Association of General Practitioners in Oncology)
Open AccessArticle
The Impact of the Pandemic on the Quality of Colorectal and Anal Cancer Care, and 2-Year Clinical Outcomes
by
Melanie Powis, Rinku Sutradhar, Simron Singh, Shabbir Alibhai, Saidah Hack, Abed Baiad, Kevin Chen, Huaqi Li, Zuhal Mohmand and Monika K. Krzyzanowska
Curr. Oncol. 2024, 31(4), 2328-2340; https://doi.org/10.3390/curroncol31040173 - 19 Apr 2024
Abstract
We undertook a retrospective study to compare the quality of care delivered to a cohort of newly diagnosed adults with colon, rectal or anal cancer during the early phase of COVID-19 (02/20–12/20) relative to the same period in the year prior (the comparator
[...] Read more.
We undertook a retrospective study to compare the quality of care delivered to a cohort of newly diagnosed adults with colon, rectal or anal cancer during the early phase of COVID-19 (02/20–12/20) relative to the same period in the year prior (the comparator cohort), and examine the impact of the pandemic on 2-year disease progression and all-cause mortality. We observed poorer performance on a number of quality measures, such as approximately three times as many patients in the COVID-19 cohort experienced 30-day post-surgical readmission (10.5% vs. 3.6%; SD:0.27). Despite these differences, we observed no statistically significant adjusted associations between COVID-19 and time to either all-cause mortality (HR: 0.88, 95% CI: 0.61–1.27, p = 0.50) or disease progression (HR: 1.16, 95% CI: 0.82–1.64, p = 0.41). However, there was a substantial reduction in new patient consults during the early phase of COVID-19 (12.2% decrease), which appeared to disproportionally impact patients who traditionally experience sociodemographic disparities in access to care, given that the COVID-19 cohort skewed younger and there were fewer patients from neighborhoods with the highest Housing and Dwelling, ands Age and Labour Force marginalization quintiles. Future work is needed to understand the more downstream effects of COVID-19 related changes on cancer care to inform planning for future disruptions in care.
Full article
(This article belongs to the Section Gastrointestinal Oncology)
►▼
Show Figures
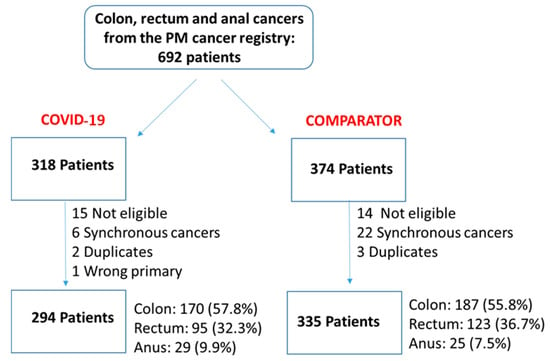
Figure 1
Open AccessReview
Antibody–Drug Conjugates in the Treatment of Genitourinary Cancers: An Updated Review of Data
by
Prathana Nathan, Adnan Rajeh, Meh Noor, Gabriel Boldt and Ricardo Fernandes
Curr. Oncol. 2024, 31(4), 2316-2327; https://doi.org/10.3390/curroncol31040172 - 19 Apr 2024
Abstract
The treatment landscape of genitourinary cancers has significantly evolved over the past few years. Renal cell carcinoma, bladder cancer, and prostate cancer are the most common genitourinary malignancies. Recent advancements have produced new targeted therapies, particularly antibody–drug conjugates (ADCs), due to a better
[...] Read more.
The treatment landscape of genitourinary cancers has significantly evolved over the past few years. Renal cell carcinoma, bladder cancer, and prostate cancer are the most common genitourinary malignancies. Recent advancements have produced new targeted therapies, particularly antibody–drug conjugates (ADCs), due to a better understanding of the underlying oncogenic factors and molecular mechanisms involved. ADCs function as a ‘drug delivery into the tumor’ system. They are composed of an antigen-directed antibody linked to a cytotoxic drug that releases cytotoxic components after binding to the tumor cell’s surface antigen. ADCs have been proven to be extremely promising in the treatment of several cancer types. For GU cancers, this novel treatment has only benefited patients with metastatic urothelial cancer (mUC). The rest of the GU cancer paradigm does not have any FDA-approved ADC treatment options available yet. In this study, we have thoroughly completed a narrative review of the current literature and summarized preclinical studies and clinical trials that evaluated the utility, activity, and toxicity of ADCs in GU cancers, the prospects of ADC development, and the ongoing clinical trials. Prospective clinical trials, retrospective studies, case reports, and scoping reviews were included.
Full article
(This article belongs to the Special Issue The Evolving Role of Antibody Drug Conjugates in Cancer Therapy)
►▼
Show Figures
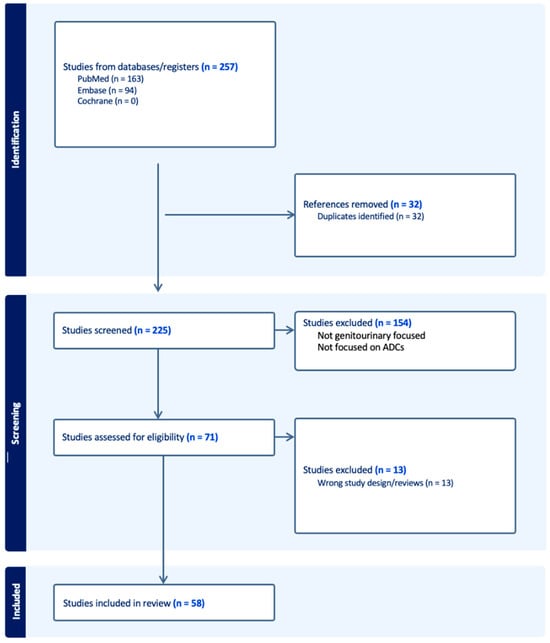
Figure 1
Open AccessFeature PaperArticle
Impact of Pregnancy on Breast Cancer Features and Prognosis
by
Valentina E. Bounous, Carola Minella, Luca Fuso, Silvia Actis, Greta Petroni, Luca G. Sgrò, Martina Borghese, Nicoletta Tomasi Cont, Riccardo Ponzone and Annamaria Ferrero
Curr. Oncol. 2024, 31(4), 2305-2315; https://doi.org/10.3390/curroncol31040171 - 19 Apr 2024
Abstract
►▼
Show Figures
Background: pregnancy-associated breast cancer (PABC) affects one in 3000 pregnancies, often presenting with aggressive features. Methods: We retrospectively evaluated a cohort of 282 young BC patients (≤45 years old) treated between 1995 and 2019, dividing them into three groups: nulliparous women, women with
[...] Read more.
Background: pregnancy-associated breast cancer (PABC) affects one in 3000 pregnancies, often presenting with aggressive features. Methods: We retrospectively evaluated a cohort of 282 young BC patients (≤45 years old) treated between 1995 and 2019, dividing them into three groups: nulliparous women, women with PABC (diagnosed within 2 years since last pregnancy) and women with BC diagnosed > 2 years since last pregnancy. This last group was further stratified according to the time between pregnancy and BC. The analysis encompassed histological factors (tumor size, histotype, grading, nodal involvement, multifocality, lympho-vascular invasion, hormone receptor expression, Ki-67 index, and HER2 expression), type of surgery and recurrence. Results: Age at diagnosis was younger in nulliparous than in parous women (p < 0.001). No significant differences were noticed regarding histological characteristics and recurrences. At univariate analysis, nodal involvement (OR = 2.4; p < 0.0001), high tumor grade (OR = 2.6; p = 0.01), and lympho-vascular invasion (OR = 2.3; p < 0.05), but not pregnancy (OR = 0.8; p = 0.30), influenced DFS negatively. Multivariate analysis confirmed nodal involvement as the only negative independent prognostic factor for a worse DFS (OR = 2.4; p = 0.0001). Conclusions: in our experience, pregnancy is not an independent adverse prognostic factor for BC DFS.
Full article
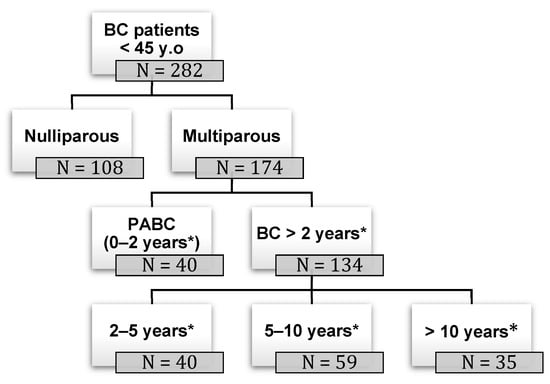
Figure 1
Open AccessArticle
Quality-of-Life Assessment in Pediatric Advanced Cancer: Development of the Patient-Reported Outcome Measure Advance QoL
by
Lye-Ann Robichaud, Julie Felipe, Michel Duval, Bruno Michon, Marianne Olivier-D’Avignon, Sébastien Perreault, Mathias Tyo-Gomez, Marc-Antoine Marquis and Serge Sultan
Curr. Oncol. 2024, 31(4), 2289-2304; https://doi.org/10.3390/curroncol31040170 - 19 Apr 2024
Abstract
►▼
Show Figures
A recent measure was developed to assess the Quality of Life (QoL) of young people with advanced cancer and is available for parents and professionals (Advance QoL). The present study aimed to elaborate self-reported versions for children and adolescents with advanced
[...] Read more.
A recent measure was developed to assess the Quality of Life (QoL) of young people with advanced cancer and is available for parents and professionals (Advance QoL). The present study aimed to elaborate self-reported versions for children and adolescents with advanced cancer. We adopted a four-phase research plan: (1) to elaborate the Advance QoL questionnaire for youth (8–12 and 13–18 years old) with a team of young research partners; (2) to evaluate the understandability of these versions in a sample of 12 young patients from the target population using cognitive interviews; (3) to assess social validity in the same group using a questionnaire and the content validity index (CVI); and (4) to refine the questionnaires according to these results. Four major themes were identified: (1) issues affecting the understanding of the tool; (2) issues that did not affect the understanding of the tool; (3) modifications to improve the tool; and (4) positive features of the tool. Advance QoL was well received, and feedback was positive. Adjustments were made according to young people’s comments and two self-reported versions are now available. It is essential to measure the key domains of QoL in advanced cancer. Advance QoL self-report versions will help target the specific needs of young people with this condition and their families.
Full article
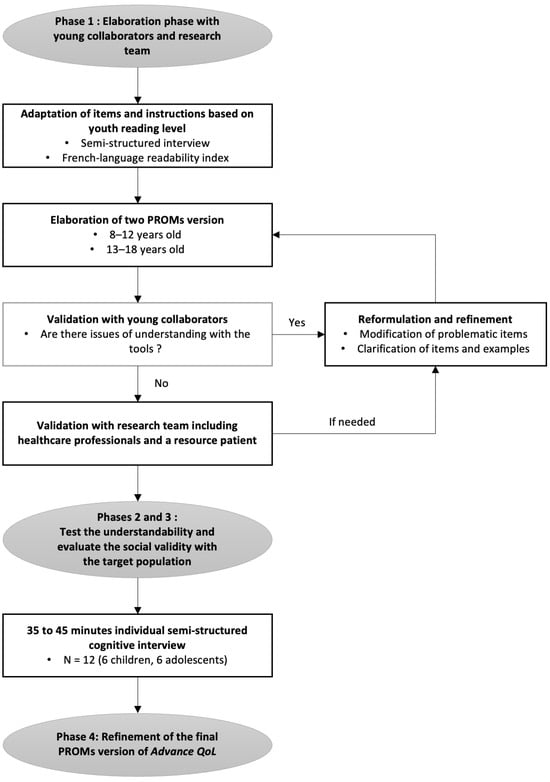
Figure 1
Open AccessArticle
Deep Learning Prediction of Axillary Lymph Node Metastasis in Breast Cancer Patients Using Clinical Implication-Applied Preprocessed CT Images
by
Tae Yong Park, Lyo Min Kwon, Jini Hyeon, Bum-Joo Cho and Bum Jun Kim
Curr. Oncol. 2024, 31(4), 2278-2288; https://doi.org/10.3390/curroncol31040169 - 18 Apr 2024
Abstract
►▼
Show Figures
Background: Accurate detection of axillary lymph node (ALN) metastases in breast cancer is crucial for clinical staging and treatment planning. This study aims to develop a deep learning model using clinical implication-applied preprocessed computed tomography (CT) images to enhance the prediction of ALN
[...] Read more.
Background: Accurate detection of axillary lymph node (ALN) metastases in breast cancer is crucial for clinical staging and treatment planning. This study aims to develop a deep learning model using clinical implication-applied preprocessed computed tomography (CT) images to enhance the prediction of ALN metastasis in breast cancer patients. Methods: A total of 1128 axial CT images of ALN (538 malignant and 590 benign lymph nodes) were collected from 523 breast cancer patients who underwent preoperative CT scans between January 2012 and July 2022 at Hallym University Medical Center. To develop an optimal deep learning model for distinguishing metastatic ALN from benign ALN, a CT image preprocessing protocol with clinical implications and two different cropping methods (fixed size crop [FSC] method and adjustable square crop [ASC] method) were employed. The images were analyzed using three different convolutional neural network (CNN) architectures (ResNet, DenseNet, and EfficientNet). Ensemble methods involving and combining the selection of the two best-performing CNN architectures from each cropping method were applied to generate the final result. Results: For the two different cropping methods, DenseNet consistently outperformed ResNet and EfficientNet. The area under the receiver operating characteristic curve (AUROC) for DenseNet, using the FSC and ASC methods, was 0.934 and 0.939, respectively. The ensemble model, which combines the performance of the DenseNet121 architecture for both cropping methods, delivered outstanding results with an AUROC of 0.968, an accuracy of 0.938, a sensitivity of 0.980, and a specificity of 0.903. Furthermore, distinct trends observed in gradient-weighted class activation mapping images with the two cropping methods suggest that our deep learning model not only evaluates the lymph node itself, but also distinguishes subtler changes in lymph node margin and adjacent soft tissue, which often elude human interpretation. Conclusions: This research demonstrates the promising performance of a deep learning model in accurately detecting malignant ALNs in breast cancer patients using CT images. The integration of clinical considerations into image processing and the utilization of ensemble methods further improved diagnostic precision.
Full article
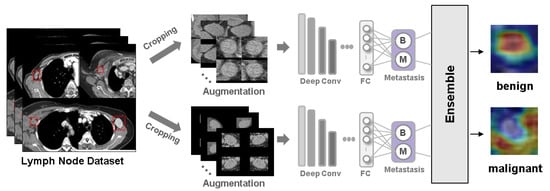
Figure 1
Open AccessCase Report
Visceral Leishmaniasis Masquerading as Drug-Induced Pancytopenia in Lung Cancer Patients
by
Sophie Laroumagne, Julie Tronchetti, Hervé Dutau and Philippe Astoul
Curr. Oncol. 2024, 31(4), 2274-2277; https://doi.org/10.3390/curroncol31040168 - 17 Apr 2024
Abstract
Maintenance chemotherapy is a standard treatment in patients with non-progressive advance staged IV non-squamous non-small cell lung cancer after induction therapy. Here, we report the case of a 53-year-old man undergoing a maintenance monotherapy with pemetrexed who presented prolonged pancytopenia despite filgrastim injections.
[...] Read more.
Maintenance chemotherapy is a standard treatment in patients with non-progressive advance staged IV non-squamous non-small cell lung cancer after induction therapy. Here, we report the case of a 53-year-old man undergoing a maintenance monotherapy with pemetrexed who presented prolonged pancytopenia despite filgrastim injections. A bone marrow aspiration revealed a macrophage activation syndrome with Leishmania amastigotes. A Polymerase Chest Reaction testing confirmed the diagnosis of visceral leishmaniasis. Treatment with liposomal amphotericin B was started. Oncologists should bear in mind that visceral leishmaniasis in endemic areas can potentially induce severe and prolonged pancytopenia in immunosuppressed patients, during chemotherapy in particular.
Full article
(This article belongs to the Section Thoracic Oncology)
►▼
Show Figures
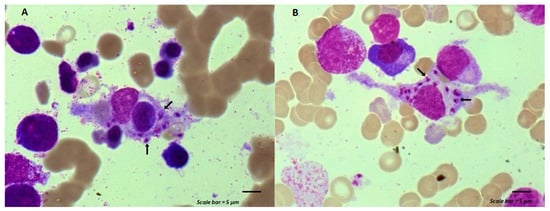
Figure 1
Open AccessReview
Multimodal Approaches to Patient Selection for Pancreas Cancer Surgery
by
Hala Muaddi, LaDonna Kearse and Susanne Warner
Curr. Oncol. 2024, 31(4), 2260-2273; https://doi.org/10.3390/curroncol31040167 - 15 Apr 2024
Abstract
With an overall 5-year survival rate of 12%, pancreas ductal adenocarcinoma (PDAC) is an aggressive cancer that claims more than 50,000 patient lives each year in the United States alone. Even those few patients who undergo curative-intent resection with favorable pathology reports are
[...] Read more.
With an overall 5-year survival rate of 12%, pancreas ductal adenocarcinoma (PDAC) is an aggressive cancer that claims more than 50,000 patient lives each year in the United States alone. Even those few patients who undergo curative-intent resection with favorable pathology reports are likely to experience recurrence within the first two years after surgery and ultimately die from their cancer. We hypothesize that risk factors for these early recurrences can be identified with thorough preoperative staging, thus enabling proper patient selection for surgical resection and avoiding unnecessary harm. Herein, we review evidence supporting multidisciplinary and multimodality staging, comprehensive neoadjuvant treatment strategies, and optimal patient selection for curative-intent surgical resections. We further review data generated from our standardized approach at the Mayo Clinic and extrapolate to inform potential future investigations.
Full article
(This article belongs to the Special Issue New Treatments in Pancreatic Ductal Adenocarcinoma)
►▼
Show Figures
Figure 1
Open AccessArticle
An Evaluation of Racial and Ethnic Representation in Research Conducted with Young Adults Diagnosed with Cancer: Challenges and Considerations for Building More Equitable and Inclusive Research Practices
by
Sharon H. J. Hou, Anika Petrella, Joshua Tulk, Amanda Wurz, Catherine M. Sabiston, Jackie Bender, Norma D’Agostino, Karine Chalifour, Geoff Eaton, Sheila N. Garland and Fiona S. M. Schulte
Curr. Oncol. 2024, 31(4), 2244-2259; https://doi.org/10.3390/curroncol31040166 - 15 Apr 2024
Abstract
The psychosocial outcomes of adolescents and young adults (AYAs) diagnosed with cancer are poorer compared to their peers without cancer. However, AYAs with cancer from diverse racial and ethnic groups have been under-represented in research, which contributes to an incomplete understanding of the
[...] Read more.
The psychosocial outcomes of adolescents and young adults (AYAs) diagnosed with cancer are poorer compared to their peers without cancer. However, AYAs with cancer from diverse racial and ethnic groups have been under-represented in research, which contributes to an incomplete understanding of the psychosocial outcomes of all AYAs with cancer. This paper evaluated the racial and ethnic representation in research on AYAs diagnosed with cancer using observational, cross-sectional data from the large Young Adults with Cancer in Their Prime (YACPRIME) study. The purpose was to better understand the psychosocial outcomes for those from diverse racial and ethnic groups. A total of 622 participants with a mean age of 34.15 years completed an online survey, including measures of post-traumatic growth, quality of life, psychological distress, and social support. Of this sample, 2% (n = 13) of the participants self-identified as Indigenous, 3% (n = 21) as Asian, 3% (n = 20) as “other,” 4% (n = 25) as multi-racial, and 87% (n = 543) as White. A one-way ANOVA indicated a statistically significant difference between racial and ethnic groups in relation to spiritual change, a subscale of post-traumatic growth, F(4,548) = 6.02, p < 0.001. Post hoc analyses showed that those under the “other” category endorsed greater levels of spiritual change than those who identified as multi-racial (p < 0.001, 95% CI = [2.49,7.09]) and those who identified as White (p < 0.001, 95% CI = [1.60,5.04]). Similarly, participants that identified as Indigenous endorsed greater levels of spiritual change than those that identified as White (p = 0.03, 95% CI = [1.16,4.08]) and those that identified as multi-racial (p = 0.005, 95% CI = [1.10,6.07]). We provided an extensive discussion on the challenges and limitations of interpreting these findings, given the unequal and small sample sizes across groups. We concluded by outlining key recommendations for researchers to move towards greater equity, inclusivity, and culturally responsiveness in future work.
Full article
(This article belongs to the Section Childhood, Adolescent and Young Adult Oncology)
Open AccessArticle
Survival Outcome Prediction in Glioblastoma: Insights from MRI Radiomics
by
Effrosyni I. Styliara, Loukas G. Astrakas, George Alexiou, Vasileios G. Xydis, Anastasia Zikou, Georgios Kafritsas, Spyridon Voulgaris and Maria I. Argyropoulou
Curr. Oncol. 2024, 31(4), 2233-2243; https://doi.org/10.3390/curroncol31040165 - 14 Apr 2024
Abstract
►▼
Show Figures
Background: Extracting multiregional radiomic features from multiparametric MRI for predicting pretreatment survival in isocitrate dehydrogenase (IDH) wild-type glioblastoma (GBM) patients is a promising approach. Methods: MRI data from 49 IDH wild-type glioblastoma patients pre-treatment were utilized. Diffusion and perfusion maps were generated, and
[...] Read more.
Background: Extracting multiregional radiomic features from multiparametric MRI for predicting pretreatment survival in isocitrate dehydrogenase (IDH) wild-type glioblastoma (GBM) patients is a promising approach. Methods: MRI data from 49 IDH wild-type glioblastoma patients pre-treatment were utilized. Diffusion and perfusion maps were generated, and tumor subregions segmented. Radiomic features were extracted for each tissue type and map. Feature selection on 1862 radiomic features identified 25 significant features. The Cox proportional-hazards model with LASSO regularization was used to perform survival analysis. Internal and external validation used a 38-patient training cohort and an 11-patient validation cohort. Statistical significance was set at p < 0.05. Results: Age and six radiomic features (shape and first and second order) from T1W, diffusion, and perfusion maps contributed to the final model. Findings suggest that a small necrotic subregion, inhomogeneous vascularization in the solid non-enhancing subregion, and edema-related tissue damage in the enhancing and edema subregions are linked to poor survival. The model’s C-Index was 0.66 (95% C.I. 0.54–0.80). External validation demonstrated good accuracy (AUC > 0.65) at all time points. Conclusions: Radiomics analysis, utilizing segmented perfusion and diffusion maps, provide predictive indicators of survival in IDH wild-type glioblastoma patients, revealing associations with microstructural and vascular heterogeneity in the tumor.
Full article
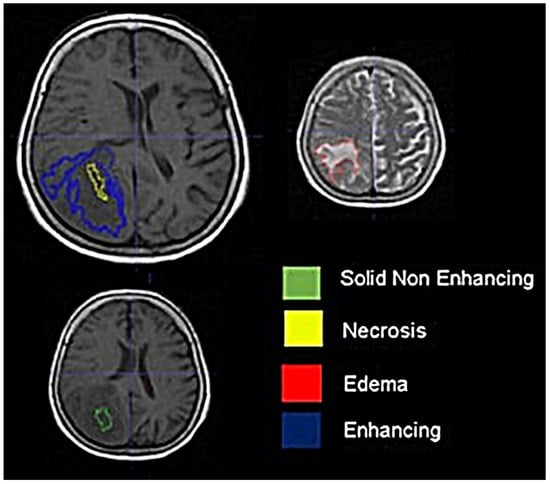
Figure 1
Open AccessArticle
The Level of Agreement between Self-Assessments and Examiner Assessments of Melanocytic Nevus Counts: Findings from an Evaluation of 4548 Double Assessments
by
Olaf Gefeller, Isabelle Kaiser, Emily M. Brockmann, Wolfgang Uter and Annette B. Pfahlberg
Curr. Oncol. 2024, 31(4), 2221-2232; https://doi.org/10.3390/curroncol31040164 - 13 Apr 2024
Abstract
Cutaneous melanoma (CM) is a candidate for screening programs because its prognosis is excellent when diagnosed at an early disease stage. Targeted screening of those at high risk for developing CM, a cost-effective alternative to population-wide screening, requires valid procedures to identify the
[...] Read more.
Cutaneous melanoma (CM) is a candidate for screening programs because its prognosis is excellent when diagnosed at an early disease stage. Targeted screening of those at high risk for developing CM, a cost-effective alternative to population-wide screening, requires valid procedures to identify the high-risk group. Self-assessment of the number of nevi has been suggested as a component of such procedures, but its validity has not yet been established. We analyzed the level of agreement between self-assessments and examiner assessments of the number of melanocytic nevi in the area between the wrist and the shoulder of both arms based on 4548 study subjects in whom mutually blinded double counting of nevi was performed. Nevus counting followed the IARC protocol. Study subjects received written instructions, photographs, a mirror, and a “nevometer” to support self-assessment of nevi larger than 2 mm. Nevus counts were categorized based on the quintiles of the distribution into five levels, defining a nevus score. Cohen’s weighted kappa coefficient (κ) was estimated to measure the level of agreement. In the total sample, the agreement between self-assessments and examiner assessments was moderate (weighted κ = 0.596). Self-assessed nevus counts were higher than those determined by trained examiners (mean difference: 3.33 nevi). The level of agreement was independent of sociodemographic and cutaneous factors; however, participants’ eye color had a significant impact on the level of agreement. Our findings show that even with comprehensive guidance, only a moderate level of agreement between self-assessed and examiner-assessed nevus counts can be achieved. Self-assessed nevus information does not appear to be reliable enough to be used in individual risk assessment to target screening activities.
Full article
(This article belongs to the Special Issue Epidemiology and Risk Factors of Skin Cancer)
►▼
Show Figures
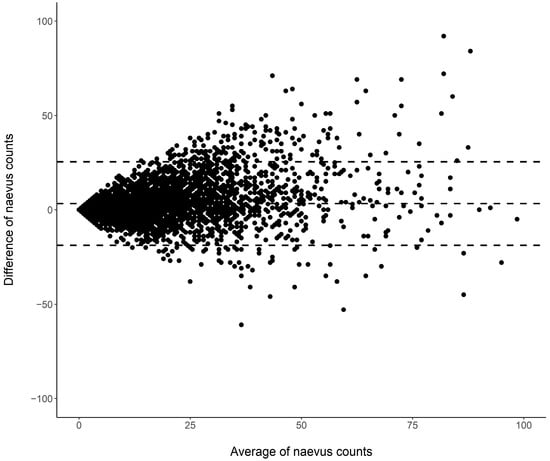
Figure 1
Open AccessSystematic Review
Active Surveillance in Non-Muscle Invasive Bladder Cancer, the Potential Role of Biomarkers: A Systematic Review
by
Diego Parrao, Nemecio Lizana, Catalina Saavedra, Matías Larrañaga, Carolina B. Lindsay, Ignacio F. San Francisco and Juan Cristóbal Bravo
Curr. Oncol. 2024, 31(4), 2201-2220; https://doi.org/10.3390/curroncol31040163 - 12 Apr 2024
Abstract
Bladder cancer (BC) is the tenth most common cause of cancer worldwide and is the thirteenth leading cause of cancer mortality. The non-muscle invasive (NMI) variant represents 75% of cases and has a mortality rate of less than 1%; however, it has a
[...] Read more.
Bladder cancer (BC) is the tenth most common cause of cancer worldwide and is the thirteenth leading cause of cancer mortality. The non-muscle invasive (NMI) variant represents 75% of cases and has a mortality rate of less than 1%; however, it has a high recurrence rate. The gold standard of management is transurethral resection in the case of new lesions. However, this is associated with significant morbidity and costs, so the reduction of these procedures would contribute to reducing complications, morbidity, and the burden to the health system associated with therapy. In this clinical scenario, strategies such as active surveillance have emerged that propose to manage low-risk BC with follow-up; however, due to the low evidence available, this is a strategy that is underutilized by clinicians. On the other hand, in the era of biomarkers, it is increasingly known how to use them as a tool in BC. Therefore, the aim of this review is to provide to clinical practitioners the evidence available to date on AS and the potential role of biomarkers in this therapeutic strategy in patients with low-grade/risk NMIBC. This is the first review linking use of biomarkers and active surveillance, including 29 articles.
Full article
(This article belongs to the Special Issue Surveillance and Active Monitoring Strategies for Cancer: Sometimes Less Is More)
►▼
Show Figures
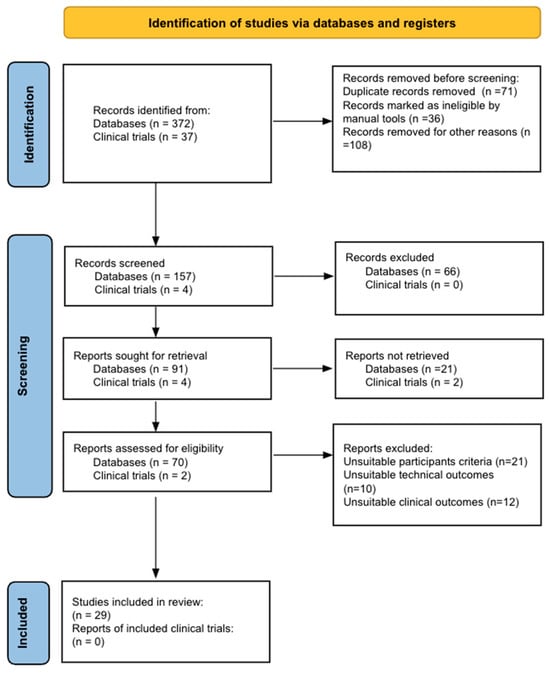
Figure 1
Open AccessReview
Prehabilitation in Adults Undergoing Cancer Surgery: A Comprehensive Review on Rationale, Methodology, and Measures of Effectiveness
by
Carlos E. Guerra-Londono, Juan P. Cata, Katherine Nowak and Vijaya Gottumukkala
Curr. Oncol. 2024, 31(4), 2185-2200; https://doi.org/10.3390/curroncol31040162 - 09 Apr 2024
Abstract
Cancer surgery places a significant burden on a patients’ functional status and quality of life. In addition, cancer surgery is fraught with postoperative complications, themselves influenced by a patient’s functional status. Prehabilitation is a unimodal or multimodal strategy that aims to increase a
[...] Read more.
Cancer surgery places a significant burden on a patients’ functional status and quality of life. In addition, cancer surgery is fraught with postoperative complications, themselves influenced by a patient’s functional status. Prehabilitation is a unimodal or multimodal strategy that aims to increase a patient’s functional capacity to reduce postoperative complications and improve postoperative recovery and quality of life. In most cases, it involves exercise, nutrition, and anxiety-reducing interventions. The impact of prehabilitation has been explored in several types of cancer surgery, most commonly colorectal and thoracic. Overall, the existing evidence suggests prehabilitation improves physiological outcomes (e.g., lean body mass, maximal oxygen consumption) as well as clinical outcomes (e.g., postoperative complications, quality of life). Notably, the benefit of prehabilitation is additional to that of enhanced recovery after surgery (ERAS) programs. While safe, prehabilitation programs require multidisciplinary coordination preoperatively. Despite the existence of numerous systematic reviews and meta-analyses, the certainty of evidence demonstrating the efficacy and safety of prehabilitation is low to moderate, principally due to significant methodological heterogeneity and small sample sizes. There is a need for more large-scale multicenter randomized controlled trials to draw strong clinical recommendations.
Full article
(This article belongs to the Section Surgical Oncology)
►▼
Show Figures
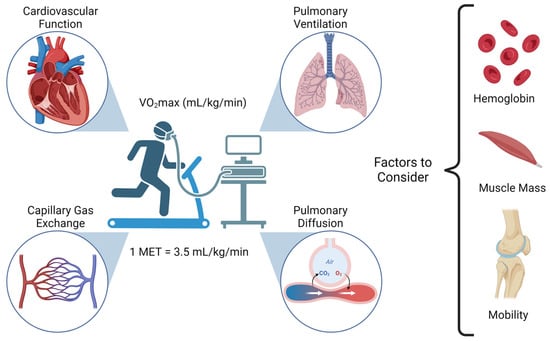
Figure 1
Open AccessArticle
Real-World Treatment Patterns and Clinical Outcomes among Patients Receiving CDK4/6 Inhibitors for Metastatic Breast Cancer in a Canadian Setting Using AI-Extracted Data
by
Ruth Moulson, Guillaume Feugère, Tracy S. Moreira-Lucas, Florence Dequen, Jessica Weiss, Janet Smith and Christine Brezden-Masley
Curr. Oncol. 2024, 31(4), 2172-2184; https://doi.org/10.3390/curroncol31040161 - 09 Apr 2024
Abstract
Cyclin-dependent kinase 4/6 inhibitors (CDK4/6i) are widely used in patients with hormone receptor-positive (HR+)/human epidermal growth factor receptor 2 negative (HER2−) advanced/metastatic breast cancer (ABC/MBC) in first line (1L), but little is known about their real-world use and clinical outcomes long-term, in Canada.
[...] Read more.
Cyclin-dependent kinase 4/6 inhibitors (CDK4/6i) are widely used in patients with hormone receptor-positive (HR+)/human epidermal growth factor receptor 2 negative (HER2−) advanced/metastatic breast cancer (ABC/MBC) in first line (1L), but little is known about their real-world use and clinical outcomes long-term, in Canada. This study used Pentavere’s previously validated artificial intelligence (AI) to extract real-world data on the treatment patterns and outcomes of patients receiving CDK4/6i+endocrine therapy (ET) for HR+/HER2− ABC/MBC at Sinai Health in Toronto, Canada. Between 1 January 2016 and 1 July 2021, 48 patients were diagnosed with HR+/HER2− ABC/MBC and received CDK4/6i + ET. A total of 38 out of 48 patients received CDK4/6i + ET in 1L, of which 34 of the 38 (89.5%) received palbociclib + ET. In 2L, 12 of the 21 (57.1%) patients received CDK4/6i + ET, of which 58.3% received abemaciclib. In 3L, most patients received chemotherapy (10/12, 83.3%). For the patients receiving CDK4/6i in 1L, the median (95% CI) time to the next treatment was 42.3 (41.2, NA) months. The median (95% CI) time to chemotherapy was 46.5 (41.4, NA) months. The two-year overall survival (95% CI) was 97.4% (92.4, 100.0), and the median (range) follow-up was 28.7 (3.4–67.6) months. Despite the limitations inherent in real-world studies and a limited number of patients, these AI-extracted data complement previous studies, demonstrating the effectiveness of CDK4/6i + ET in the Canadian real-world 1L, with most patients receiving palbociclib as CDK4/6i in 1L.
Full article
(This article belongs to the Topic Artificial Intelligence in Cancer, Biology and Oncology)
►▼
Show Figures
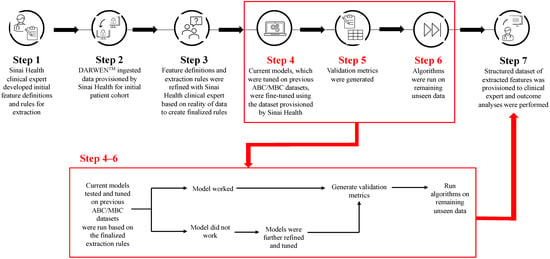
Figure 1

Journal Menu
► ▼ Journal Menu-
- Current Oncology Home
- Aims & Scope
- Editorial Board
- Reviewer Board
- Topical Advisory Panel
- Instructions for Authors
- Special Issues
- Topics
- Sections & Collections
- Article Processing Charge
- Indexing & Archiving
- Editor’s Choice Articles
- Most Cited & Viewed
- Journal Statistics
- Journal History
- Journal Awards
- Society Collaborations
- Conferences
- Editorial Office
Journal Browser
► ▼ Journal Browser-
arrow_forward_ios
Forthcoming issue
arrow_forward_ios Current issue - Volumes not published by MDPI
Highly Accessed Articles
Latest Books
E-Mail Alert
News
Topics
Topic in
Biology, Cancers, Current Oncology, Diseases, JCM, Pathogens
Pathogenetic, Diagnostic and Therapeutic Perspectives in Head and Neck Cancer
Topic Editors: Shun-Fa Yang, Ming-Hsien ChienDeadline: 20 June 2024
Topic in
Cancers, Cells, JCM, Radiation, Pharmaceutics, Applied Sciences, Nanomaterials, Current Oncology
Innovative Radiation Therapies
Topic Editors: Gérard Baldacchino, Eric Deutsch, Marie Dutreix, Sandrine Lacombe, Erika Porcel, Charlotte Robert, Emmanuelle Bourneuf, João Santos Sousa, Aurélien de la LandeDeadline: 30 June 2024
Topic in
Cancers, Diagnostics, JCM, Current Oncology, Gastrointestinal Disorders, Biomedicines
Hepatobiliary and Pancreatic Diseases: Novel Strategies of Diagnosis and Treatments
Topic Editors: Alessandro Coppola, Damiano Caputo, Roberta Angelico, Domenech Asbun, Chiara MazzarelliDeadline: 20 July 2024
Topic in
Cancers, Catalysts, Current Oncology, Plasma, Sci
Advances in Low-Temperature Plasma Cancer Therapy
Topic Editors: Michael Keidar, Li Lin, Dayun YanDeadline: 20 September 2024

Conferences
Special Issues
Special Issue in
Current Oncology
The Clinical Trials and Management of Acute Myeloid Leukemia
Guest Editor: Margaret T. KasnerDeadline: 26 April 2024
Special Issue in
Current Oncology
Liver Transplantation for Cancer: The Future of Transplant Oncology
Guest Editor: Tomoharu YoshizumiDeadline: 30 April 2024
Special Issue in
Current Oncology
An Update on Surgical Treatment for Hepato-Pancreato-Biliary Cancers
Guest Editors: Nikolaos Machairas, Stylianos Kykalos, Dimitrios SchizasDeadline: 15 May 2024
Special Issue in
Current Oncology
Surgery Advances in Gynecologic Tumors
Guest Editor: Allan L. CovensDeadline: 31 May 2024
Topical Collections
Topical Collection in
Current Oncology
Editorial Board Members’ Collection Series: Contemporary Perioperative Concepts in Cancer Surgery
Collection Editors: Vijaya Gottumukkala, Jörg Kleeff
Topical Collection in
Current Oncology
Editorial Board Members’ Collection Series in "Exercise and Cancer Management"
Collection Editors: Linda Denehy, Ravi Mehrotra, Nicole Culos-Reed
Topical Collection in
Current Oncology
New Insights into Prostate Cancer Diagnosis and Treatment
Collection Editor: Sazan Rasul
Topical Collection in
Current Oncology
New Insights into Breast Cancer Diagnosis and Treatment
Collection Editors: Filippo Pesapane, Matteo Suter